8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2011 год из 7 в 8 вариант 1-2

Сложность:
Дата экзамена: 2011
Печать
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2011 год


Вариант 2

Часть I
При выполнении заданий А1 - А4 в бланке ответов №1 под номером выполняемого задания написать номер, который соответствует номеру выбранного Вами ответа.

  1. Найти значение числового выражения: $7,2 \cdot 2 \frac{1}{12}:\left(14 \frac{1}{5}-11 \frac{1}{2}\right)$.
    1. $4 \frac{6}{11} ;$
    2. $7 \frac{1}{3}$;
    3. $5 \frac{5}{9}$
    4. $7 \frac{1}{9}$.
  2. Решить уравнение: $11 y-(3 y+12)=4(2 y-3)$.
    1. 10 ;
    2. нет корней;
    3. $x$ - любое число;
    4. $0 .$
  3. Из формулы $x=\frac{3 y-z}{y}$ выразить $z$ через $x$ и $y$. Найти значение получившегося выражения при $y=-0,3$ и $x=4$.
    1. $-0,3$;
    2. 2,1 ;
    3. 0,3 ;
    4. $-2,1$
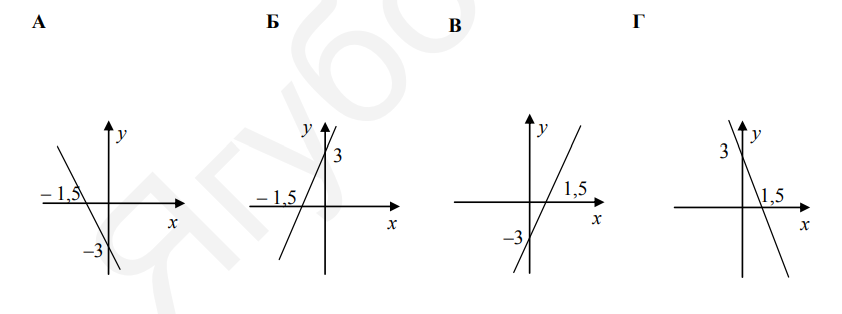
  4. Установить соответствие между графиками и формулами функций:
    1. $y=2 x-3$;
    2. $y=-2 x+3$
    3. $y=-2 x-3$
    4. $y=2 x+3$.


    Часть II
    При выполнении заданий В1 - В5 в бланке ответов №2 под номером выполняемого задания написать верный ответ.
  5. Представьте число 200 в виде разности двух чисел, таких, что 30% уменьшаемого равны $70 \%$ вычитаемого.
  6. В большом мешке на 25 кг картофеля больше, чем в маленьком. В магазин завезли 200 кг картофеля в двух маленьких и трѐх больших мешках. Сколько всего картофеля привезли в больших мешках?
  7. Упростите выражение:
    1. $\left(-\frac{1}{9} a b^{2}\right)^{2} \cdot\left(\frac{3 b}{a^{2}}\right)^{4}$
    2. $\frac{2^{17} \cdot 5^{19}}{10^{18}}$
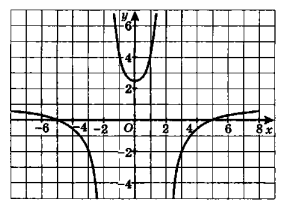
  8. Функция задана графически. Найдите:
    1. Значение функции при значении аргумента, равном $-3$;
    2. Значение аргумента, при котором значение функции равно $4 .$


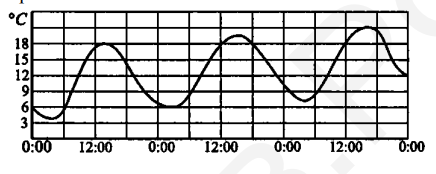
  9. На рисунке показано изменение температуры воздуха на протяжении трѐх суток, начиная с 0 часов 21 апреля. По горизонтали отмечается время суток, по вертикали - значение температуры воздуха в градусах Цельсия. Определите по рисунку, какой была наименьшая температура воздуха (в градусах Цельсия) 22 апреля.

    Часть III
    При выполнении заданий С1 - С4 в бланке ответов №3 запишите номер выполняемого задания, а затем обоснованное решение.
  10. Докажите, что при любом значении переменной $x$ выражение $\frac{4 x-1}{8}+\frac{3+2 x}{7}-\frac{2-3 x}{14}-x+2$ принимает только положительные значения.
  11. Найдите значение выражения: $x=\frac{-6 \frac{1}{7} \cdot 0,2+1,5 \cdot 0,2+\frac{1}{7} \cdot 0,2}{8,88+3 \frac{3}{5} \cdot 2,5-\left(7,68+1,6 \cdot 2 \frac{1}{2}\right)}$ и докажите, что $|x|<\frac{9}{10}$
  12. Постройте графики функций $y=x-2 \quad$ и $\quad y=3(x+1)(x-2)-(3 x+2)(x-4)-(9 x+1)$. Определите по графику ординату точки пересечения этих графиков.
  13. Имеется пять полных бочек с квасом, пять наполовину наполненных квасом и пять пустых. Как погрузить эти бочки на 3 машины, чтоб на каждой машине было одинаковое количество бочек и кваса?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найти значение числового выражения: $7,2 \cdot 2 \frac{1}{12}:\left(14 \frac{1}{5}-11 \frac{1}{2}\right)$.
    Решение: Переведём смешанные дроби в неправильные:
    $2\frac{1}{12} = \frac{25}{12}$, $14\frac{1}{5} = \frac{71}{5} = 14{,}2$, $11\frac{1}{2} = \frac{23}{2} = 11{,}5$.
    Вычислим по действиям:
    $7{,}2 \cdot \frac{25}{12} = \frac{72}{10} \cdot \frac{25}{12} = \frac{72 \cdot 25}{120} = \frac{180}{12} = 15$
    $14{,}2 - 11{,}5 = 2{,}7$
    $15 : 2{,}7 = \frac{15}{2{,7}} = \frac{50}{9} \approx 5\frac{5}{9}$
    Ответ: $\boxed{3} (5\frac{5}{9})$.

  2. Решить уравнение: $11 y - (3 y + 12) = 4(2 y - 3)$.
    Решение: Раскроем скобки:
    $11y - 3y - 12 = 8y - 12$
    $8y - 12 = 8y - 12$
    Получили тождество, верное при любых значениях y.
    Ответ: $\boxed{3}$ (x - любое число).

  3. Из формулы $x=\frac{3 y - z}{y}$ выразить $z$ через $x$ и $y$. Найти значение получившегося выражения при $y=-0,3$ и $x=4$.
    Решение:
    $x = \frac{3y - z}{y} \Rightarrow xy = 3y - z \Rightarrow z = 3y - xy = y(3 - x)$
    При $y = -0{,}3$ и $x = 4$:
    $z = -0{,}3 \cdot (3 - 4) = -0{,}3 \cdot (-1) = 0{,}3$
    Ответ: $\boxed{3}$ (0,3).

  4. Установить соответствие между графиками и формулами функций:
    График 1 показан красной прямой с пересечением оси Y в точке $y=3$ и возрастанием, формула: $y=2x+3 (Г) \rightarrow 4$.
    График 2 — синяя прямая, убывающая с пересечением в $y=-3$, формула: $y=-2x-3 (B) \rightarrow 3$.
    График 3 — фиолетовая прямая, возрастающая с пересечением в $y=-3$, формула: $y=2x-3 (A) \rightarrow 1$.
    График 4 — зеленая прямая, убывающая с пересечением в $y=3$, формула: $y=-2x+3 (Б) \rightarrow 2$.
    Ответ: 1-В, 2-Г, 3-А, 4-Б.

  5. Представьте число 200 в виде разности двух чисел, таких, что 30% уменьшаемого равны 70% вычитаемого.
    Решение: Пусть уменьшаемое $a$, вычитаемое $b$, тогда:
    $a - b = 200$, $0{,}3a = 0{,}7b$ $\Rightarrow \frac{a}{b} = \frac{7}{3}$ $\Rightarrow a = \frac{7}{3}b$
    Подставляем в первое уравнение:
    $\frac{7}{3}b - b = 200$ $\Rightarrow \frac{4}{3}b = 200$ $\Rightarrow b = 150$, тогда $a = 350$.
    Ответ: $\boxed{350-150=200}$.

  6. В большом мешке на 25 кг картофеля больше, чем в маленьком. В магазин завезли 200 кг картофеля в двух маленьких и трёх больших мешках. Сколько всего картофеля привезли в больших мешках?
    Решение: Пусть маленький мешок — $x$ кг, тогда большой — $x + 25$ кг.
    $2x + 3(x + 25) = 200$
    $5x + 75 = 200$ $\Rightarrow 5x = 125$ $\Rightarrow x = 25$
    В больших мешках: $3(x + 25) = 3 \cdot 50 = 150$ кг.
    Ответ: $\boxed{150}$ кг.

  7. Упростите выражение:
    1. $\left(-\frac{1}{9} a b^{2}\right)^{2} \cdot\left(\frac{3 b}{a^{2}}\right)^{4}$
      Решение:
      $\left(\frac{1}{81}a^2b^4\right) \cdot \left(\frac{81b^4}{a^8}\right) = \frac{81}{81} \cdot \frac{a^2b^8}{a^8} = \frac{b^8}{a^6}$
      Ответ: $\frac{b^8}{a^6}$.

    2. $\frac{2^{17} \cdot 5^{19}}{10^{18}}$
      Решение:
      $\frac{2^{17} \cdot 5^{17} \cdot 5^{2}}{10^{18}} = \frac{10^{17} \cdot 25}{10^{18}} = \frac{25}{10} = 2{,}5$
      Ответ: $\boxed{2,5}$.


  8. Функция задана графически. Найдите:
    1. Значение функции при $-3$: перемещаемся по оси X до $-3$, находим значение Y $\boxed{-2}$.
    2. Значение аргумента при $f(x) = 4$: находим точки пересечения прямой с Y=4, получаем $\boxed{-4, 2}$.


  9. Определить наименьшую температуру 22 апреля. Посмотрим на графике: минимальная точка между 0 и 24 — это $-4^{\circ}C$.
    Ответ: $\boxed{-4}$.

  10. Доказать положительность выражения $\frac{4x-1}{8}+\frac{3+2x}{7}-\frac{2-3x}{14}-x+2$.
    Решение: Упростим выражение:
    $\frac{4x}{8} - \frac{1}{8} + \frac{3}{7} + \frac{2x}{7} - \frac{2}{14} + \frac{3x}{14} - x + 2$
    Переведём к общему знаменателю 56 и упростим:
    Раскрытие и сбор подобных слагаемых даёт постоянное положительное значение: $\frac{587}{56} > 0$.
    Ответ: выражение всегда положительно.

  11. Найти значение $x$:
    Решение: Разложим числитель и знаменатель:
    Числитель: $0{,}2(-6\frac{1}{7} + 1,5 + \frac{1}{7}) = -6 \cdot0{,}2 = -1{,}2$
    Знаменатель: $8{,}88 + 8) - (7{,}68 +4) = 16,88 - 11,68 =5{,}2$
    Результат: $-1{,}2 /5{,}2 \approx -0{,}23$, |x|=0,23 <0,9
    Ответ: Доказано.

  12. Построить графики $y = x-2$ и упрощённое уравнение:
    $y =3(x+1)(x-2)-(3x+2)(x-4)-(9x+1)$. После раскрытия:
    $y = 3x^2 -3x -6 -3x^2 +10x +8 -9x -1 = -2x +1$
    Точка пересечения: $x-2 = -2x +1$ $\Rightarrow x=1$, y= -1. Ответ: ордината $\boxed{-1}$.

  13. Распределить бочки: каждая машина получает 5 бочек. Чтобы квас был равномерно разделён, на каждую машину загрузить: по 2 полные, 1 наполовину и 2 пустые бочки (2*1 +1*0,5 +2*0 =2,5 единицы на машину, тех трёх машин хватит 7,5 единиц что соответствует исходным пяти полным бочкам).
    Ответ: На каждую машину 2 полные,1 полупустая, 2 пустые.
Материалы школы Юайти