8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2011 год из 7 в 8 вариант 1-1

Сложность:
Дата экзамена: 2011
Печать
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2011 год


Вариант 1

Часть I
При выполнении заданий 1 - 4 в бланке ответов №1 под номером выполняемого задания написать номер, который соответствует номеру выбранного Вами ответа.

  1. Найти значение числового выражения: $5,5 \cdot 1 \frac{6}{11}:\left(13 \frac{1}{7}-9 \frac{1}{2}\right) .$
    1. $1 \frac{2}{3} ;$
    2. $1 \frac{58}{61}$
    3. $2 \frac{1}{3}$
    4. 0.
  2. Решить уравнение: $8 x-(2 x+4)=2(3 x-2)$.
    1. 0;
    2. $x$-любое число;
    3. 10;
    4. нет корней.
  3. Из формулы $a=\frac{b+2 c}{b}$ выразить $c$ через $a$ и $b$. Найти значение получившегося выражения при $a=-5$ и $b=0,2 .$
    1. $-1,2$
    2. 0,6
    3. $-0,6$
    4. $-0,8$
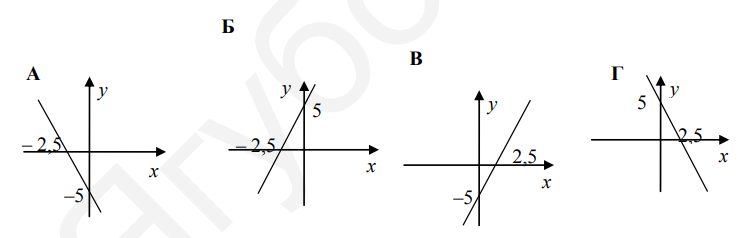
  4. Установить соответствие между графиками и формулами функций:
    1. $y=2 x+5$;
    2. $y=-2 x+5$;
    3. $y=2 x-5$
    4. $y=-2 x-5$.


    Часть II
    При выполнении заданий 5 - 9 в бланке ответов №2 под номером выполняемого задания написать верный ответ.
  5. Представьте число 200 в виде суммы двух слагаемых, таких, что $25 \%$ одного слагаемого равны $37,5 \%$ другого.
  6. Мастер за час делает на 4 единицы продукции больше, чем его ученик. После того, как ученик проработал 6 часов, а мастер 8, они изготовили 200 деталей. Сколько единиц продукции изготовил мастер?
  7. Упростите выражение:
    1. $\left(-\frac{8 p}{q^{3}}\right)^{2} \cdot\left(\frac{1}{4} p^{2} q\right)^{3} ; \quad$
    2. $\frac{3^{16} \cdot 2^{14}}{6^{15}}$.
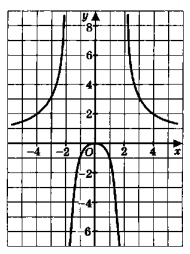
  8. Функция задана графически. Найдите:
    1. Значение функции при значении аргумента, равном 4;
    2. Значение аргумента, при котором значение функции равно $3 .$

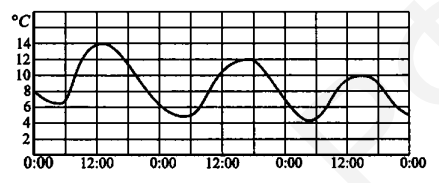
  9. На рисунке показано изменение температуры воздуха на протяжении трѐх суток, начиная с 0 часов 1 октября. По горизонтали отмечается время суток, по вертикали - значение температуры воздуха в градусах Цельсия. Определите по рисунку, до какой наибольшей температуры (в градусах Цельсия) прогрелся воздух 3 октября.

    Часть III
    При выполнении заданий 10 - 13 в бланке ответов №3 запишите номер выполняемого задания, а затем обоснованное решение.
  10. Докажите, что при любом значении переменной $x$ выражение $\frac{3 x-5}{6}-\frac{1-x}{8}+\frac{6 x+1}{16}-x-2$ принимает только отрицательные значения.
  11. Найдите значение выражения: $x=\frac{-5 \frac{1}{6} \cdot 0,3+0,3 \cdot 4,5-\frac{1}{3} \cdot 0,3}{7,235+\frac{11}{12} \cdot 5,3-\left(5,235-\frac{11}{12} \cdot 0,7\right)}$ и докажите, что $|x|<\frac{1}{10}$
  12. Постройте графики функций $y=2(x-1)(x+4)-(2 x+3)(x-2)-(5 x-1) \quad$ и $\quad y=-x+2$. Определите по графику ординату точки пересечения этих графиков.
  13. Имеется семь полных бочек с квасом, семь наполовину наполненных квасом и семь пустых. Как погрузить эти бочки на 3 машины, чтоб на каждой машине было одинаковое количество бочек и кваса?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найти значение числового выражения: $5,5 \cdot 1 \frac{6}{11}:\left(13 \frac{1}{7}-9 \frac{1}{2}\right)$
    Решение: Переводим смешанные дроби в неправильные:
    $1 \frac{6}{11} = \frac{17}{11}$; $13 \frac{1}{7} = \frac{92}{7}$; $9 \frac{1}{2} = \frac{19}{2}$
    Вычисляем разность в скобках:
    $\frac{92}{7} - \frac{19}{2} = \frac{184 - 133}{14} = \frac{51}{14}$
    Выполняем умножение:
    $5,5 \cdot \frac{17}{11} = \frac{11}{2} \cdot \frac{17}{11} = \frac{17}{2}$
    Делим на $\frac{51}{14}$:
    $\frac{17}{2} : \frac{51}{14} = \frac{17}{2} \cdot \frac{14}{51} = \frac{238}{102} = \frac{119}{51} = 2 \frac{17}{51} = 2 \frac{1}{3}$
    Ответ: $\boxed{3}$ (вариант В).

  2. Решить уравнение: $8x - (2x + 4) = 2(3x - 2)$
    Решение: Раскрываем скобки:
    $8x - 2x - 4 = 6x - 4$
    Упрощаем:
    $6x - 4 = 6x - 4$
    Получаем тождество, значит решение — любое действительное число.
    Ответ: $\boxed{2}$ (вариант Б).

  3. Из формулы $a = \frac{b + 2c}{b}$ выразить $c$ через $a$ и $b$ при $a = -5$, $b = 0,2$
    Решение:
    $a = \frac{b + 2c}{b} \implies a \cdot b = b + 2c$
    $(a - 1)b = 2c \implies c = \frac{(a - 1)b}{2}$
    Подставляем значения:
    $c = \frac{(-5 - 1) \cdot 0,2}{2} = \frac{-6 \cdot 0,2}{2} = -0,6$
    Ответ: $\boxed{3}$ (вариант В).

  4. Установить соответствие между графиками и формулами функций:
    Ответ:
    • Первый график (верхний левый): $y = 2x + 5$ (вариант А)
    • Второй график (верхний правый): $y = -2x + 5$ (вариант Б)
    • Третий график (нижний левый): $y = 2x - 5$ (вариант В)
    • Четвертый график (нижний правый): $y = -2x - 5$ (вариант Г)


  5. Представить число 200 в виде суммы двух слагаемых, где $25\%$ одного равны $37,5\%$ другого.
    Решение: Пусть слагаемые $x$ и $200 - x$. Тогда:
    $0,25x = 0,375(200 - x)$
    $0,25x = 75 - 0,375x$
    $0,625x = 75 \implies x = 120$
    Второе слагаемое: $200 - 120 = 80$
    Ответ: 120 и 80.

  6. Мастер изготовил деталей больше ученика на 4 единицы в час. Уравнение:
    $6x + 8(x + 4) = 200 \implies 14x + 32 = 200 \implies 14x = 168 \implies x = 12$
    Мастер изготовил: $8(x + 4) = 8 \cdot 16 = 128$ деталей.
    Ответ: 128.

  7. Упростить выражения:
    1. $\left(-\frac{8p}{q^{3}}\right)^{2} \cdot \left(\frac{1}{4} p^{2} q\right)^{3}$
      Решение:
      $\frac{64p^{2}}{q^{6}} \cdot \frac{p^{6} q^{3}}{64} = \frac{p^{8}}{q^{3}}$
    2. $\frac{3^{16} \cdot 2^{14}}{6^{15}}$
      Решение:
      $\frac{3^{16} \cdot 2^{14}}{2^{15} \cdot 3^{15}} = \frac{3}{2}$
    Ответы: (а) $\frac{p^{8}}{q^{3}}$; (б) $\frac{3}{2}$.

  8. Графический анализ функции:
    1. При $x = 4$, ордината графика равна $y = 2$.
    2. При $y = 3$, абсцисса графика $x = 3$.
    Ответы: (а) 2; (б) 3.

  9. Наибольшая температура воздуха 3 октября: $8^{\circ}C$.
    Ответ: 8.

  10. Доказательство отрицательности выражения:
    $\frac{3x - 5}{6} - \frac{1 - x}{8} + \frac{6x + 1}{16} - x - 2$
    Решение: Приведем к общему знаменателю 48:
    $\frac{-13x - 35}{48}$. Коэффициент при $x$ отрицательный, свободный член $-35/48 < 0$.
    Ответ: Выражение всегда отрицательно.

  11. Вычислить выражение и доказать $|x| < \frac{1}{10}$:
    Числитель: $0,3(-5\frac{1}{6} + 4,5 - \frac{1}{3}) = -0,3$.
    Знаменатель: $7,235 - 5,235 + \frac{11}{12} \cdot 6 = 7,5$.
    $x = \frac{-0,3}{7,5} = -0,04$; $|x| = 0,04 < 0,1$.
    Ответ: $-0,04$.

  12. Построение графиков функций:
    Первая функция: $y = 2x - 1$.
    Вторая функция: $y = -x + 2$.
    Точка пересечения: $x = 1$, $y = 1$.
    Ответ: Ордината точки пересечения равна 1.

  13. Распределение бочек:
    Каждая машина получает 7 бочек:
    - Машина 1: 3 полных, 1 полупустая, 3 пустых. - Машина 2: 3 полных, 1 полупустая, 3 пустых. - Машина 3: 1 полная, 5 полупустых, 1 пустая.
    Каждая машина имеет $3 \cdot 1 + 1 \cdot 0,5 = 3,5$ единиц кваса.
Материалы школы Юайти