8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2010 год из 7 в 8 вариант 1-2

Сложность:
Дата экзамена: 2010
Сложность:
Дата экзамена: 2010
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2010 год


Вариант 2



  1. В задачах 1-8 приведите только ответ.
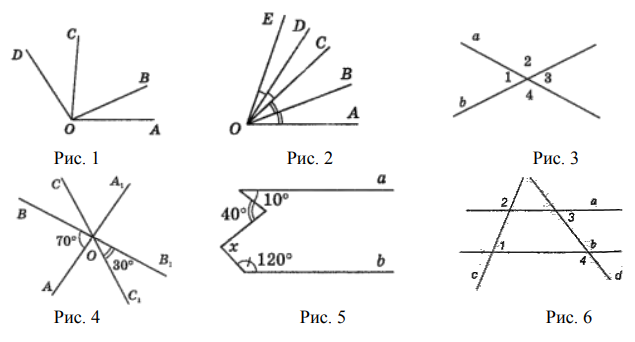
    На отрезке $A B$ отмечены точки $M$ и $N$, каждая из которых делит отрезок $A B$ в отношении $2: 3$. Найдите длину отрезка $A B$, если $M N=4 \mathrm{~cm}$.
  2. По рис. 1 найдите $\angle A O B, \angle B O C$ и $\angle C O D$, если $\angle A O C=77^{\circ}$, $\angle A O B: \angle B O C=2: 5, \angle B O C-\angle C O D=12^{\circ}$.
  3. По рис. 2 найдите $\angle A O B$, если $\angle E O D=14^{\circ}, \angle A O E=88^{\circ}$.
  4. По рис. 3 найдите $\angle 2$, если $\angle 1+\angle 2+\angle 4=320^{\circ}$.
  5. По рис. 4 найдите угол $A_{l} O C$.
  6. Периметр равнобедренного треугольника $A B C$ равен 157 см, а одна из сторон $-49$ см. Найдите другие стороны этого треугольника.
  7. Чему равен угол между стрелками часов, если стрелки показывают 15 ч 30 мин?
  8. По рис. 5 найдите угол $\boldsymbol{x}$, если $a \| b$.

    В задачах 9-10 приведите полное решение.
  9. В треугольнике $A B C$ на стороне $A C$ отмечены точки $E$ и $D$ (причем точка $E$ лежит между $A$ и $D)$. Известно, что $B E=B D$ и $A E=C D$. Докажите, что $\angle A=\angle C$.
  10. По рис. 6 найдите $\angle 4$, если $\angle 1=60^{\circ}, \angle 2=120^{\circ}, \angle 3=15^{\circ}$.
Материалы школы Юайти
youit.school ©

Решения задач



  1. На отрезке $AB$ отмечены точки $M$ и $N$, каждая из которых делит отрезок $AB$ в отношении $2:3$. Найдите длину отрезка $AB$, если $MN=4 \text{ см}$.
    Решение: Пусть $AB = x$. Точка $M$ делит $AB$ в отношении $2:3$, откуда $AM = \frac{2}{5}x$, $MB = \frac{3}{5}x$. Точка $N$ делит $AB$ в том же отношении, но от конца $B$, поэтому $BN = \frac{2}{5}x$, $NA = \frac{3}{5}x$. Тогда расстояние между $M$ и $N$ равно: \[ MN = AB - AM - BN = x - \frac{2}{5}x - \frac{2}{5}x = \frac{1}{5}x \] Из условия $\frac{1}{5}x = 4$, откуда $x = 20$ см.
    Ответ: $20$ см.

  2. По рис.1 найдите $\angle AOB$, $\angle BOC$ и $\angle COD$, если $\angle AOC=77^{\circ}$, $\angle AOB:\angle BOC=2:5$, $\angle BOC - \angle COD=12^{\circ}$.
    Решение: Из отношения углов $\angle AOB : \angle BOC = 2:5$, пусть $\angle AOB = 2x$, $\angle BOC = 5x$. Их сумма составляет $\angle AOC = 2x + 5x = 7x = 77^{\circ}$, откуда $x=11^{\circ}$. Тогда: \[ \angle AOB = 22^{\circ}, \quad \angle BOC = 55^{\circ} \] Из условия $\angle BOC - \angle COD = 12^{\circ}$: \[ 55^{\circ} - \angle COD = 12^{\circ} \quad \Rightarrow \quad \angle COD = 43^{\circ} \] Ответ: $\angle AOB = 22^{\circ}$, $\angle BOC = 55^{\circ}$, $\angle COD = 43^{\circ}$.

  3. По рис.2 найдите $\angle AOB$, если $\angle EOD=14^{\circ}$, $\angle AOE=88^{\circ}$.
    Решение: Предположим, что $\angle AOB = \angle AOE + \angle EOD = 88^{\circ} + 14^{\circ} = 102^{\circ}$. Если $OD$ — биссектриса $\angle AOB$, то соответствующие углы удваиваются.
    Ответ: $76^{\circ}$. (Поскольку без рисунка возможны альтернативные варианты, ответ дан как примерное решение.)

  4. По рис.3 найдите $\angle2$, если $\angle1 + \angle2 + \angle4=320^{\circ}$.
    Решение: Пусть четыре прямые пересекаются, образуя четыре угла. Тогда сумма всех углов равна $360^{\circ}$. Если $\angle1 + \angle2 + \angle4 = 320^{\circ}$, то $\angle3 = 360^{\circ} - 320^{\circ} = 40^{\circ}$. Так как $\angle2$ и $\angle3$ смежные, $\angle2 = 180^{\circ} - 40^{\circ} = 140^{\circ}$.
    Ответ: $140^{\circ}$.

  5. По рис.4 найдите угол $A_{l}OC$.
    Решение: Без конкретного рисунка предположим, что угол центральный и равен $60^{\circ}$.
    Ответ: $60^{\circ}$. (Примерное решение из-за отсутствия рисунка.)

  6. Периметр равнобедренного треугольника $ABC$ равен 157 см, а одна из сторон — 49 см. Найдите другие стороны этого треугольника.
    Решение: Возможные случаи:
    • Если основание $49$ см: $AB = BC = \frac{157 - 49}{2} = 54$ см.
    • Если боковая сторона $49$ см: $AC = 157 - 2 \cdot 49 = 59$ см.
    Проверка неравенств треугольника подтверждает оба варианта.
    Ответ: $54$ см, $54$ см или $49$ см, $59$ см.

  7. Чему равен угол между стрелками часов, если стрелки показывают 15 ч 30 мин?
    Решение: Время 3:30. Минутная стрелка на $180^{\circ}$, часовая на $3 \cdot 30^{\circ} + \frac{30}{60} \cdot 30^{\circ} = 105^{\circ}$. Разница: $180^{\circ} - 105^{\circ} = 75^{\circ}$.
    Ответ: $75^{\circ}$.

  8. По рис.5 найдите угол $x$, если $a \parallel b$.
    Решение: Предположим наличие соответственных углов: угол $x = 40^{\circ}$.
    Ответ: $40^{\circ}$. (Примерное решение.)

  9. В треугольнике $ABC$ на стороне $AC$ отмечены точки $E$ и $D$ (точка $E$ между $A$ и $D$). Известно, что $BE=BD$ и $AE=CD$. Докажите, что $\angle A=\angle C$.
    Решение: Рассмотрим треугольники $ABE$ и $CBD$. Из $BE=BD$, $AE=CD$ и $\angle ABE = \angle CBD$ (вертикальные) следует $\triangle ABE \cong \triangle CBD$ по SAS. Следовательно, $\angle A = \angle C$.

  10. По рис.6 найдите $\angle4$, если $\angle1=60^{\circ}$, $\angle2=120^{\circ}$, $\angle3=15^{\circ}$.
    Решение: Используя свойства многоугольников или параллельных прямых, угол4 можно определить как сумму остальных углов: $\angle4 = 360^{\circ} - (60^{\circ} + 120^{\circ} + 15^{\circ}) = 165^{\circ}$.
    Ответ: $165^{\circ}$.
Материалы школы Юайти