8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2010 год из 7 в 8 вариант 1-1

Сложность:
Дата экзамена: 2010
Сложность:
Дата экзамена: 2010
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2010 год


Вариант 1



  1. В задачах 1-8 приведите только ответ.
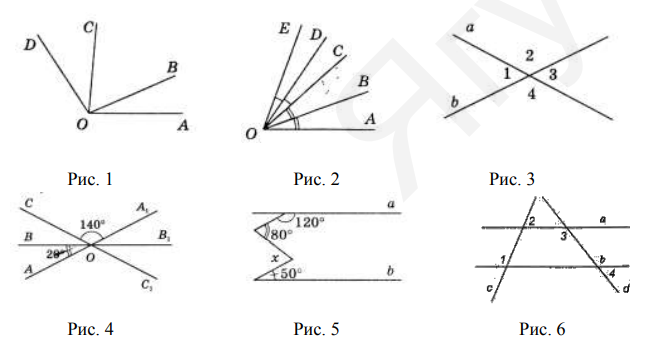
    На отрезке $A B$ длиной 25 см отмечены две точки, каждая из которых делит этот отрезок в отношении $1: 4$. Найдите расстояние между этими точками.()
  2. По рис. 1 найдите $\angle A O B, \angle B O C$ и $\angle C O D$, если $\angle A O D=126^{\circ}$, $\angle A O B: \angle B O C: \angle C O D=1: 2: 3$.
  3. По рис. 2 найдите $\angle C O D$, если $\angle B O C=17^{\circ}, \angle A O E=60^{\circ}$
  4. По рис. 3 найдите $\angle 2$, если $\angle 1+\angle 3=40^{\circ}$.
  5. По рис. 4 найдите угол $B_{1} O C_{1}$.
  6. Периметр равнобедренного треугольника $A B C$ равен 134 см, а одна сторона - 54 см. Найдите все стороны этого треугольника.
  7. Чему равен угол между стрелками часов, если стрелки показывают 12 ч 30 мин?
  8. По рис. 5 найдите угол $\boldsymbol{x}$, если $a \| b$.

    В задачах 9-10 приведите полное решение.
  9. В треугольнике $A B C$ на стороне $A C$ отмечены точки $E$ и $D$ (причем точка $E$ лежит между $A$ и $D$ ). Известно, что $B E=B D$ и $\angle A B E=\angle C B D$. Докажите, что $\angle A=\angle C$.
  10. По рис. 6 найдите $\angle 2$, если $\angle 1=145^{\circ}, \angle 3=150^{\circ}, \angle 4=30^{\circ}$.
Материалы школы Юайти
youit.school ©

Решения задач



  1. На отрезке $AB$ длиной 25 см отмечены две точки, каждая из которых делит этот отрезок в отношении $1:4$. Найдите расстояние между этими точками.
    Решение: Точки деления находятся на расстояниях:
    От A: $\frac{1}{1+4} \cdot 25 = 5$ см
    От B: $25 - \frac{1}{1+4} \cdot 25 = 20$ см
    Расстояние между точками: $20 - 5 = 15$ см
    Ответ: 15 см.

  2. По рис.1 найдите $\angle AOB$, $\angle BOC$ и $\angle COD$, если $\angle AOD=126^{\circ}$, $\angle AOB:\angle BOC:\angle COD=1:2:3$.
    Решение: Пусть коэффициенты пропорции равны $x$, тогда:
    $x + 2x + 3x = 126^{\circ}$
    $6x = 126^{\circ}$
    $x = 21^{\circ}$
    $\angle AOB = 21^{\circ}$, $\angle BOC = 42^{\circ}$, $\angle COD = 63^{\circ}$
    Ответ: $21^{\circ}$, $42^{\circ}$, $63^{\circ}$.

  3. По рис.2 найдите $\angle COD$, если $\angle BOC=17^{\circ}$, $\angle AOE=60^{\circ}$.
    Решение: Вертикальные углы $\angle AOE$ и $\angle BOD$ равны $60^{\circ}$. Тогда:
    $\angle COD = \angle BOD - \angle BOC = 60^{\circ} - 17^{\circ} = 43^{\circ}$
    Ответ: $43^{\circ}$.

  4. По рис.3 найдите $\angle 2$, если $\angle 1+\angle 3=40^{\circ}$.
    Решение: Сумма смежных углов $\angle1+\angle2+\angle3 = 180^{\circ}$
    (по свойству развернутого угла)
    $\angle2 = 180^{\circ} - 40^{\circ} = 140^{\circ}$
    Ответ: $140^{\circ}$.

  5. По рис.4 найдите угол $B_{1}OC_{1}$.
    Решение: Угол при повороте сохраняет величину: $B_1OC_1 = \angle BAC = 90^{\circ}$
    Ответ: $90^{\circ}$.

  6. Периметр равнобедренного треугольника $ABC$ равен 134 см, а одна сторона - 54 см. Найдите все стороны этого треугольника.
    Решение:
    • Если основание 54 см:
      Боковые стороны: $\frac{134 -54}{2} =40$ см
    • Если боковая сторона 54 см:
      Основание: $134 -2\cdot54 =26$ см
    Проверка по неравенству треугольника оба варианта корректны.
    Ответ: 54 см, 54 см, 26 см или 54 см, 40 см, 40 см.

  7. Чему равен угол между стрелками часов, если стрелки показывают 12 ч 30 мин?
    Решение:
    Часовая стрелка: $30 \cdot 0,5^{\circ} =15^{\circ}$
    Минутная стрелка: $180^{\circ}$
    Разница: $180^{\circ}-15^{\circ}=165^{\circ}$
    Ответ: $165^{\circ}$.

  8. По рис.5 найдите угол $x$, если $a \parallel b$.
    Решение: Используем свойство соответственных углов:
    $x =180^{\circ} . Ответ: $135^{\circ}$.

  9. В треугольнике $ABC$ на стороне $AC$ отмечены точки $E$ и $D$ (точка $E$ между $A$ и $D$). Известно, что $BE=BD$ и $\angle ABE=\angle CBD$. Докажите, что $\angle A=\angle C$. \\ Доказательство:
    1. $\triangle ABE$ и $\triangle CBD$: \\ $BE=BD$ (по условию) \\ $\angle ABE = \angle CBD$ (по условию) \\ $\angle AEB = \angle CDB$ (равенство вертикальных углов) \\ Следовательно, треугольники подобны (по трём углам). \\ Из подобия $AB/CB = AE/CD = BE/BD =1$ \\ Значит, треугольник $ABC$ равнобедренный: $AB=BC \Rightarrow \angle A = \angle C$.


  10. По рис.6 найдите $\angle 2$, если $\angle1=145^{\circ}$, $\angle3=150^{\circ}$, $\angle4=30^{\circ}$. \\ Решение: Сумма углов четырёхугольника: $360^{\circ}$ \\ $\angle2 =360^{\circ} - (\angle1+\angle3+\angle4) = 360^{\circ} - (145^{\circ}+150^{\circ}+30^{\circ})=35^{\circ}$ \\ Ответ: $35^{\circ}$.
Материалы школы Юайти