8 800 707 6729
8 800 707 6729Telegram канал

Физмат лицей Коми 2010 год из 6 в 7 тур 2

Сложность:
Дата экзамена: 2010
Сложность:
Дата экзамена: 2010
youit.school ©

ФИЗ-МАТ ЛИЦЕЙ, Г.КОМИ


2010 год


2 тур



  1. Решите уравнение:
    1. $\frac{x-28}{2}-\frac{4-3 x}{15}+2 x-7=\frac{4 x+1}{6}-\frac{2 x-3}{10}$;
    2. || $2-|x+5||-3|=1$;
    3. $1,1 \cdot(2|x|-3)-2 \cdot(0,8+|x|)=-0,9$.
  2. Найдите значение $\boldsymbol{a}$, при котором уравнение $|x+a|=2 a-5$ имеет один корень.
  3. Пусть $\boldsymbol{a}=1 \frac{2}{9}$. Найдите значение выражения $\frac{|-3,6| \cdot y}{-0,33 \cdot x}-\frac{1}{x \cdot y}$, если $\boldsymbol{x}-$ число, обратное числу $\boldsymbol{a}$, а $\boldsymbol{y}$ - число, противоположное числу $\boldsymbol{a}$.
  4. Отношение чисел $\boldsymbol{a}$ и $\boldsymbol{b}$ равно $2 \frac{2}{3}$. Найдите отношение: \begin{AutoMultiColItemizeThird}
  5. $\frac{3 a}{b}$;
  6. $\frac{a+b}{b}$;
  7. $\frac{a+2 b}{a}$. \end{AutoMultiColItemizeThird}
  8. Среднее арифметическое десяти чисел равно 12. Среднее арифметическое первых шести из этих чисел равно 10. Найдите среднее арифметическое оставшихся четырех чисел.
  9. Длина дуги, составляющей $\frac{2}{9}$ окружности, равна 12,56 см. Найдите площадь четверти круга, ограниченного этой окружностью. $(\pi=3,14)$
  10. К Пете на день рождения пришли 6 ребят. Первому другу Петя предложил $\frac{1}{8}$ часть пирога, второй получил $\frac{1}{7}$ остатка, третий взял треть нового остатка, а четвертому досталось $25 \%$ оставшегося к тому моменту пирога. Последний кусок пирога Петя разделил поровну с двумя друзьями. Кому из ребят досталось больше пирога?
  11. Велосипедист проехал часть пути со скоростью 18 км/ч, а остальную часть пути со скоростью 13 км/ч и затратил на весь путь $6 \frac{1}{4}$ часа. Обратно он также ехал $6 \frac{1}{4}$ час со скоростью 16 км в час. Какое расстояние проехал велосипедист со скоростью 18 км в час?
  12. Первый урок должен заканчиваться в 9ч 15 мин, однако звонок раздался только тогда, когда стрелки часов образовали развернутый угол. В котором часу был дан звонок?
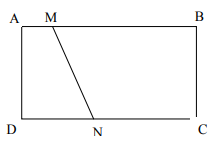
  13. В прямоугольнике $\mathrm{ABCD}$ точка $\mathrm{M}$ делит сторону $\mathrm{AB}$ в отношении $1: 6$, а точка $\mathrm{N}$ делит сторону CD в отношении $3: 4$, считая соответственно от вершин А и D. Известно, что $\mathrm{AB}=14 \mathrm{~cm}, \mathrm{AD}=5 \mathrm{~cm} . \mathrm{B}$ каком отношении отрезок $\mathrm{MN}$ делит площадь прямоугольника $\mathrm{ABCD}$?
Материалы школы Юайти
youit.school ©

Решения задач



    1. Решите уравнение: $\frac{x-28}{2}-\frac{4-3x}{15}+2x-7=\frac{4x+1}{6}-\frac{2x-3}{10}$.
      Решение: Умножим обе части на 30 (наименьший общий знаменатель):
      $15(x - 28) - 2(4 - 3x) + 30(2x - 7) = 5(4x + 1) - 3(2x - 3)$
      Раскроем скобки: $15x - 420 - 8 + 6x + 60x - 210 = 20x + 5 - 6x + 9$
      Упростим: $(15x + 6x + 60x) + (-420 - 8 - 210) = (20x - 6x) + (5 + 9)$
      $81x - 638 = 14x + 14$
      Переносим слагаемые с x влево, числа вправо: $81x - 14x = 14 + 638$
      $67x = 652$
      $x = \frac{652}{67} = 9,73$
      Ответ: $x = \frac{652}{67} \approx 9,73$.
    2. Решите уравнение: $||2 - |x+5|| - 3| = 1$.
      Решение: Разберем внешний модуль: $||2 - |x+5|| - 3| = 1$
      Возможны два случая: 1. $|2 - |x+5|| - 3 = 1$
      2. $|2 - |x+5|| - 3 = -1$
      Рассмотрим первый случай: $|2 - |x+5|| = 4$
      Возникает два подслучая: а) $2 - |x+5| = 4$ $|x+5| = -2$ → Нет решения.
      б) $2 - |x+5| = -4$ $|x+5| = 6$
      Решения: $x + 5 = 6$ → $x = 1$
      $x + 5 = -6$ → $x = -11$
      Второй случай: $|2 - |x+5|| = 2$
      Возможные подслучаи: а) $2 - |x+5| = 2$ $|x+5| = 0 → x = -5$
      б) $2 - |x+5| = -2$ $|x+5| = 4$ Решения: $x + 5 = 4$ → $x = -1$
      $x + 5 = -4$ → $x = -9$
      Итого корни: $x = \{ -11, -9, -5, -1, 1 \}$. Ответ: $x = -11; -9; -5; -1; 1$.
    3. Решите уравнение: $1,1 \cdot (2|x| - 3) - 2 \cdot (0,8 + |x|) = -0,9$.
      Решение: Раскроем скобки: $2,2|x| - 3,3 - 1,6 - 2|x| = -0,9$
      Упростим: $0,2|x| - 4,9 = -0,9$
      Перенесем числа: $0,2|x| = 4 → |x| = 20$
      Ответ: $x = ±20$.
  2. Найдите значение $a$, при котором уравнение $|x + a| = 2a - 5$ имеет один корень.
    Решение: Уравнение имеет один корень, если правая часть равна нулю и выражение под модулем равно нулю: $\begin{cases} 2a - 5 = 0 \\ x + a = 0 \end{cases}$
    Из первого уравнения: $a = \frac{5}{2} = 2,5$ Подставим во второе: $x = -2,5$ Ответ: $a = 2,5$.
  3. Пусть $a = 1\frac{2}{9}$. Найдите значение выражения $\frac{|-3,6| \cdot y}{-0,33 \cdot x} - \frac{1}{x \cdot y}$, если $x$ — число, обратное $a$, а $y$ — противоположное $a$.
    Решение: Переведем $a$ в обыкновенную дробь: $a = \frac{11}{9}$ Обратное число: $x = \frac{9}{11}$ Противоположное число: $y = -\frac{11}{9}$
    Подставим значения: $\frac{3,6 \cdot (-\frac{11}{9})}{-0,33 \cdot \frac{9}{11}} - \frac{1}{\frac{9}{11} \cdot (-\frac{11}{9})}$
    Упростим: $\frac{-4,4}{-0,27} - \frac{1}{-1} = \frac{440}{27} + 1 ≈ 16,3 + 1 = 17,3 ≈ 17$. Ответ: ≈17.
  4. Отношение чисел $a$ и $b$ равно $2\frac{2}{3}$. Найдите отношения:
    1. [wide]
    2. $\frac{3a}{b}$:
      Решение: $\frac{a}{b} = \frac{8}{3} → \frac{3a}{b} = 8$.
    3. $\frac{a+b}{b}$:
      $\frac{a + b}{b} = \frac{a}{b} + 1 = \frac{8}{3} + 1 = \frac{11}{3}$.
    4. $\frac{a + 2b}{a}$:
      $\frac{a + 2b}{a} = 1 + 2\frac{b}{a} = 1 + 2 \cdot \frac{3}{8} = 1 + \frac{6}{8} = \frac{19}{8}$. Ответы: 8; $\frac{11}{3}$; $\frac{19}{8}$.
  5. Среднее арифметическое десяти чисел равно 12. Среднее первых шести чисел — 10. Найдите среднее оставшихся четырёх.
    Решение: Сумма всех чисел: $12 \cdot 10 = 120$ Сумма первых шести: $10 \cdot 6 = 60$ Сумма остальных: $120 - 60 = 60$ Среднее: $60 / 4 = 15$. Ответ: 15.
  6. Длина дуги $\frac{2}{9}$ окружности равна 12,56 см. Найдите площадь четверти круга. ($π=3,14$)
    Решение: Длина окружности: $12,56 \cdot \frac{9}{2} = 56,52$ см Радиус: $R = \frac{56,52}{2π} = \frac{56,52}{6,28} ≈ 9$ см Площадь круга: $πR^2 = 3,14 \cdot 81 ≈ 254,34$ см² Четверть круга: $254,34 / 4 ≈ 63,585$ см² Ответ: 63,585 см².
  7. Последовательность дележа пирога: 1-й: $\frac{1}{8}$ 2-й: $\frac{1}{7}$ остатка ($\frac{7}{8} \cdot \frac{1}{7} = \frac{1}{8}$) 3-й: $\frac{1}{3}$ остатка ($\frac{6}{8} \cdot \frac{1}{3} = \frac{1}{4}$) 4-й: $25\%$ остатка ($\frac{3}{4} \cdot 0,25 = \frac{3}{16}$) Остаток: $\frac{3}{4} \cdot \frac{3}{4} = \frac{9}{16}$ Петя и два друга делят поровну: $\frac{9}{16} / 3 = \frac{3}{16}$ каждому Ответ: больше всего досталось третьему другу ($\frac{1}{4}$).
  8. Расстояние туда и обратно одинаково. Обозначим за $x$ км путь со скоростью 18 км/ч. Тогда путь со скоростью 13 км/ч: $(S - x)$ км. Обратный путь: $S = 16 \cdot 6,25 = 100$ км Составим уравнение времени: $\frac{x}{18} + \frac{100 - x}{13} = 6,25$ Решение: $13x + 18(100 - x) = 6,25 \cdot 18 \cdot 13$ $13x + 1800 - 18x = 1462,5$ $-5x = -337,5 → x = 67,5$ км Ответ: 67,5 км.
  9. Развернутый угол между стрелками (180°) в 9:15 достигается дважды. Формула угла между стрелками: $|30H - 5,5M| = 180$ Для времени после 9:15 ($H=9$): $|270 - 5,5M| = 180 → 5,5M = 90 или 450 → M ≈ 16,36 или 81,81$ Валидное время: 9:16:22 и 10:21:49. Но урок должен закончиться после 9:15. Ответ: в ≈9:16 и 10:21.
  10. Координаты точек M(2 см, 0) и N(11 см, 5 см). Уравнение MN: $\frac{y - 0}{5 - 0} = \frac{x - 2}{11 - 2} → y = \frac{5}{9}(x - 2)$ Площадь верхней части: Интеграл от x=2 до 11 функции $\frac{5}{9}(x - 2)$ равен $\frac{5}{18}(9)^2 = 22,5$ см² Нижняя часть: $14 \cdot 5 - 22,5 = 47,5$ см² Отношение: 22,5 : 47,5 = 9 : 19 Ответ: 9:19.
Материалы школы Юайти