Экономический лицей им. Г.В. Плеханова из 9 в 10 класс демовариант

1. Найдите значение выражения: \[ (7{,}9 - 12{,}1)\,\bigl(\tfrac{1}{6} - \tfrac{5}{4}\bigr). \]
2. Раскройте скобки и упростите выражение: \[ -8x - 8\bigl(-5x + 7{,}5\bigr) - 4\,(8x - 3). \]
3. Найдите значение выражения: \[ (\sqrt{27} + 4\sqrt{3})\,\sqrt{3} \;-\;(2\sqrt{8})^2. \]
4. Укажите решение неравенства: \[ (x + 2)(x - 7) > 0. \]
   1. 
      
5. В прямоугольном треугольнике \(ABC\) катет \(AC = 12\), а гипотенуза \(AB = 20\). Найдите \(\cos \angle ABC\).
6. В среднем из 50 карманных фонариков, поступивших в продажу, шесть неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарь окажется исправен.
7. На рисунке изображены графики функций вида \(y = ax^2 + bx + c\). Установите соответствие между знаками коэффициентов и графиками функций.
   
   
   КОЭФФИЦИЕНТЫ
   
   \(\displaystyle \begin{aligned} &\text{A) } a0;\quad \text{B) } a>0,\;c>0;\quad \text{C) } a>0,\;c<0. \end{aligned} \)
   
   ГРАФИКИ
   
   
   
   
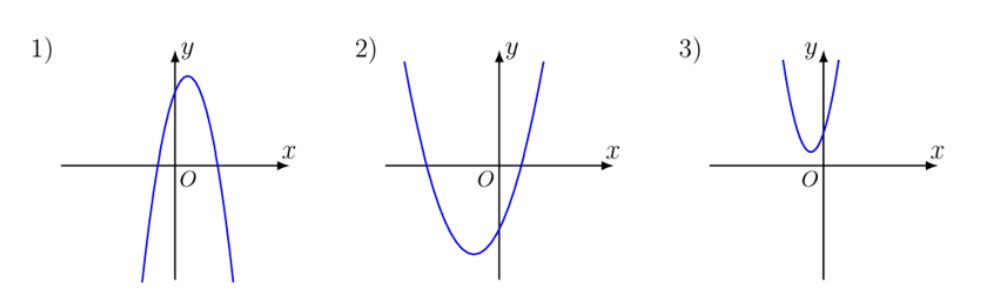
   В таблице под каждой буквой укажите соответствующий номер:
   
   \[ \] В ответе укажите последовательность трёх цифр.
8. Радиус окружности, вписанной в трапецию, равен 34. Найдите высоту этой трапеции.
9. Для выполнения заданий 9--10 используется оборотная сторона БЛАНКА ОТВЕТОВ. Необходимо оформить полное обоснование решения. Пишите аккуратно и разборчиво.
10. Решите уравнение: \[ (x-1)\,(x^2 + 6x + 9) = 5(x + 3). \] Если уравнение имеет более одного корня, в ответе запишите сумму всех корней.
11. Велосипедист выехал с постоянной скоростью из города \(A\) в город \(B\), расстояние между которыми равно 180 км. На следующий день он отправился обратно в \(A\), увеличив скорость на 5 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из \(A\) в \(B\). Найдите скорость велосипедиста на пути из \(B\) в \(A\).
12. Для выполнения задания 11 используется отдельный неразлинованный лист.
13. Перед вами расположены определённым образом фигуры и графические элементы. Перерисуйте их на отдельный неразлинованный лист максимально точно. Внимание! Все точки должны быть в том же количестве, как они представлены на образце.

Решения задач

1. Найдите значение выражения: $(7{,}9 - 12{,}1)\left(\frac{1}{6} - \frac{5}{4}\right)$
   Решение: \[ (7{,}9 - 12{,}1) = -4{,}2 \quad \text{и} \quad \frac{1}{6} - \frac{5}{4} = \frac{2}{12} - \frac{15}{12} = -\frac{13}{12} \] \[ -4{,}2 \cdot \left(-\frac{13}{12}\right) = \frac{21}{5} \cdot \frac{13}{12} = \frac{273}{60} = 4{,}55 \] Ответ: 4,55.
   
   
2. Раскройте скобки и упростите выражение: $-8x - 8(-5x + 7{,}5) - 4(8x - 3)$
   Решение: \[ -8x + 40x - 60 - 32x + 12 = (-8x + 40x - 32x) + (-60 + 12) = 0x - 48 = -48 \] Ответ: -48.
   
   
3. Найдите значение выражения: $(\sqrt{27} + 4\sqrt{3})\sqrt{3} - (2\sqrt{8})^2$
   Решение: \[ \sqrt{27} = 3\sqrt{3} \Rightarrow (3\sqrt{3} + 4\sqrt{3})\sqrt{3} = 7\sqrt{3} \cdot \sqrt{3} = 21 \] \[ (2\sqrt{8})^2 = 4 \cdot 8 = 32 \quad \Rightarrow \quad 21 - 32 = -11 \] Ответ: -11.
   
   
4. Укажите решение неравенства: $(x + 2)(x - 7) > 0$
   Решение: Метод интервалов. Корни: $x = -2$, $x = 7$. Знаки на интервалах: \[ x \in (-\infty; -2) \cup (7; +\infty) \] Ответ: вариант 1 (стрелки влево от -2 и вправо от 7).
   
   
5. В прямоугольном треугольнике $ABC$ катет $AC = 12$, гипотенуза $AB = 20$. Найдите $\cos \angle ABC$
   Решение: \[ BC = \sqrt{AB^2 - AC^2} = \sqrt{400 - 144} = 16 \quad \Rightarrow \quad \cos \angle ABC = \frac{BC}{AB} = \frac{16}{20} = 0{,}8 \] Ответ: 0,8.
   
   
6. Вероятность исправного фонарика:
   Решение: \[ \frac{50 - 6}{50} = \frac{44}{50} = 0{,}88 \] Ответ: 0,88.
   
   
7. Установите соответствие между графиками и коэффициентами:
   Решение:
   • График 1: ветви вверх ($a > 0$), пересечение с осью $y$ отрицательно ($c < 0$) → C)
   • График 2: ветви вниз ($a 0$) → A)
   • График 3: ветви вверх ($a > 0$), пересечение с осью $y$ положительно ($c > 0$) → B)
   Ответ: 231.
   
   
8. Высота трапеции:
   Решение: Радиус вписанной окружности $r = \frac{h}{2} \Rightarrow h = 2r = 68$
   Ответ: 68.
   
   
9. Решите уравнение: $(x-1)(x^2 + 6x + 9) = 5(x + 3)$
   Решение: \[ (x-1)(x+3)^2 - 5(x+3) = 0 \quad \Rightarrow \quad (x+3)[(x-1)(x+3) - 5] = 0 \] \[ x+3 = 0 \Rightarrow x = -3 \] \[ (x-1)(x+3) - 5 = x^2 + 2x - 8 = 0 \Rightarrow x = \frac{-2 \pm 6}{2} = 2 \text{ или } -4 \] Сумма корней: $-3 + 2 - 4 = -5$
   Ответ: -5.
   
   
10. Скорость велосипедиста на обратном пути:
    Решение: Пусть $v$ — скорость из $A$ в $B$, тогда: \[ \frac{180}{v} = \frac{180}{v+5} + 3 \quad \Rightarrow \quad 3v^2 + 15v - 900 = 0 \quad \Rightarrow \quad v = 15 \] Скорость обратно: $15 + 5 = 20$ км/ч
    Ответ: 20.