Экономический лицей им. Г.В. Плеханова из 9 в 10 класс 2019 год Демовариант

ЭКОНОМИЧЕСКИЙ ЛИЦЕЙ ПЛЕХАНОВА

2019 год

Демоверсия

1. (2 балла) Найдите значение выражения \[ \frac{432^2 - 568^2}{1000}. \]
2. (2 балла) Спортивный магазин проводит акцию. Любая футболка стоит 400,рублей. При покупке двух футболок действует скидка 20%. Сколько рублей придётся заплатить за покупку двух футболок?
3. (2 балла) Найдите значение выражения \[ \biggl(\frac{9^{\frac13}\,\cdot\,9^{\frac14}}{\sqrt[12]{9}}\biggr)^{3}. \]
4. (3 балла) В геометрической прогрессии сумма первого и второго членов равна 72, а сумма второго и третьего членов равна 144. Найдите первые три члена этой прогрессии.
5. (3 балла) Валя выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 51.
6. (3 балла) Радиус окружности, вписанной в правильный треугольник, равен 4. Найдите сторону этого треугольника.
7. (3 балла) Основания трапеции равны 4 и 9. Найдите отрезок, соединяющий середины диагоналей трапеции.
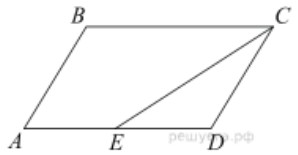
8. (4 балла) Площадь параллелограмма \(ABCD\) равна 5. Точка \(E\) — середина стороны \(AD\). Найдите площадь трапеции \(AE\,CB\).
   
9. (4 балла) Решите уравнение \[ (x^2 - 16)^2 + (x^2 + x - 12)^2 = 0. \] Если корней несколько, укажите в ответе их произведение.
10. (4 балла) Решите неравенство \[ (x - 3)^2 < \sqrt{5\,(x - 3)}. \]

Решения задач

1. Найдите значение выражения \[ \frac{432^2 - 568^2}{1000}. \] Решение: Применим формулу разности квадратов: \[ \frac{(432 - 568)(432 + 568)}{1000} = \frac{(-136) \cdot 1000}{1000} = -136. \] Ответ: \(-136\).
2. Сколько рублей придётся заплатить за покупку двух футболок?
   Решение: Стоимость двух футболок без скидки: \[ 400 \cdot 2 = 800 \text{ руб.} \] Скидка \(20\%\): \[ 800 \cdot 0,2 = 160 \text{ руб.} \] Итоговая сумма: \[ 800 - 160 = 640 \text{ руб.} \] Ответ: \(640\).
3. Найдите значение выражения \[ \biggl(\frac{9^{\frac13}\,\cdot\,9^{\frac14}}{\sqrt[12]{9}}\biggr)^{3}. \] Решение: Упростим выражение в скобках: \[ \frac{9^{\frac13 + \frac14}}{9^{\frac{1}{12}}} = \frac{9^{\frac7{12}}}{9^{\frac1{12}}} = 9^{\frac7{12} - \frac1{12}} = 9^{\frac12}. \] Возведение в степень \(3\): \[ (9^{\frac12})^3 = 9^{\frac32} = 3^{3} = 27. \] Ответ: \(27\).
4. Найдите первые три члена геометрической прогрессии.
   Решение: Пусть \(b_1 = a\), \(q\) — знаменатель прогрессии. Тогда: \[ \begin{cases} a + aq = 72 \\ aq + aq^2 = 144. \end{cases} \] Разделим второе уравнение на первое: \[ q = \frac{144}{72} = 2. \] Подставим \(q = 2\) в первое уравнение: \[ a(1 + 2) = 72 \Rightarrow a = 24. \] Члены прогрессии: \(24\), \(48\), \(96\).
   Ответ: \(24\), \(48\), \(96\).
5. Найдите вероятность того, что трёхзначное число делится на 51.
   Решение: Трёхзначных чисел: \(900\). Числа, кратные \(51\): \[ 102, 153, 204, \dots, 969. \] Количество таких чисел: \[ \left\lfloor \frac{999}{51} \right\rfloor - \left\lfloor \frac{99}{51} \right\rfloor = 19 - 1 = 18. \] Вероятность: \[ \frac{18}{900} = 0,02. \] Ответ: \(0,02\).
6. Найдите сторону треугольника.
   Решение: Формула радиуса вписанной окружности: \[ r = \frac{a\sqrt{3}}{6} \Rightarrow a = \frac{6r}{\sqrt{3}} = 8\sqrt{3}. \] Ответ: \(8\sqrt{3}\).
7. Найдите отрезок, соединяющий середины диагоналей трапеции.
   Решение: Свойство средней линии трапеции: \[ \frac{9 - 4}{2} = 2,5. \] Ответ: \(2,5\).
8. Найдите площадь трапеции \(AEBC\).
   Решение: Точка \(E\) — середина \(AD\), площадь \(EDC = \frac{1}{4} \cdot 5 = 1,25\). Площадь трапеции: \[ 5 - 1,25 = 3,75. \] Ответ: \(3,75\).
9. Решите уравнение.
   Решение: Сумма квадратов равна нулю: \[ \begin{cases} x^2 - 16 = 0 \\ x^2 + x - 12 = 0. \end{cases} \] Решения: \[ x = -4. \] Ответ: \(-4\).
10. Решите неравенство.
    Решение: Замена \(t = x - 3\), \(t \geq 0\): \[ t^2 < \sqrt{5t} \Rightarrow t(t - \sqrt{5}) < 0 \Rightarrow 0 \leq t < \sqrt{5}. \] Возвращаемся к \(x\): \[ 3 \leq x < 3 + \sqrt{5}. \] Ответ: \(x \in [3; 3 + \sqrt{5})\).