Экономический лицей им. Г.В. Плеханова из 8 в 9 класс демовариант

1. Найдите значение выражения: \[ \biggl(4\frac{2}{7} - 8\frac{3}{11}\biggr)\cdot 77. \]
2. Раскройте скобки и упростите выражение: \[ 12x - 6\bigl(2x - 3{,}2\bigr). \]
3. Найдите значение выражения: \[ (\sqrt{7} + \sqrt{3})(\sqrt{3} - \sqrt{7}). \]
4. Решите уравнение \[ x^2 - 11x + 30 = 0. \] Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
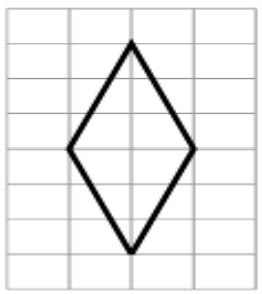
5. На клетчатой бумаге с размером клетки \(1\times1\) изображён ромб. Найдите площадь этого ромба.
   
   
   
   
   
   
   
6. В фирме такси в данный момент свободно 20 машин: 2 чёрных, 2 жёлтых и 16 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
7. Один из углов параллелограмма равен \(26^\circ\). Найдите большой угол этого параллелограмма. Ответ дайте в градусах.
8. Решите неравенство. В ответе укажите его наибольшее целое решение: \[ 3 - 2x \ge 8x - 1. \]
9. Для выполнения заданий 9–10 используется оборотная сторона БЛАНКА ОТВЕТОВ. Необходимо оформить полное обоснование решения. Пишите аккуратно и разборчиво.
10. Катет и гипотенуза прямоугольного треугольника равны 16 и 20. Найдите высоту, проведённую к гипотенузе.
11. Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 195 км — со скоростью 65 км/ч, а последние 225 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
12. Для выполнения задания 11 используется отдельный неразлинованный лист.
13. Перед вами расположены определённым образом фигуры и графические элементы. Перерисуйте их на отдельный неразлинованный лист максимально точно. Внимание! Все точки должны быть в том же количестве, как они представлены на образце.

Решения задач

1. Найдите значение выражения: \[ \biggl(4\frac{2}{7} - 8\frac{3}{11}\biggr)\cdot 77. \] Решение: Переведём смешанные числа в неправильные дроби:
   $4\frac{2}{7} = \frac{30}{7}$, $8\frac{3}{11} = \frac{91}{11}$
   Выполним вычитание: $\frac{30}{7} - \frac{91}{11} = \frac{30 \cdot 11 - 91 \cdot 7}{77} = \frac{330 - 637}{77} = -\frac{307}{77}$
   Умножим результат на 77: $-\frac{307}{77} \cdot 77 = -307$
   Ответ: -307.
2. Раскройте скобки и упростите выражение: \[ 12x - 6\bigl(2x - 3{,}2\bigr). \] Решение: Раскроем скобки:
   $12x - 6 \cdot 2x + 6 \cdot 3,2 = 12x - 12x + 19,2 = 19,2$
   Ответ: 19,2.
3. Найдите значение выражения: \[ (\sqrt{7} + \sqrt{3})(\sqrt{3} - \sqrt{7}). \] Решение: Воспользуемся формулой разности квадратов:
   $(\sqrt{3})^2 - (\sqrt{7})^2 = 3 - 7 = -4$
   Ответ: -4.
4. Решите уравнение \[ x^2 - 11x + 30 = 0. \] Решение: Найдём дискриминант:
   $D = (-11)^2 - 4 \cdot 1 \cdot 30 = 121 - 120 = 1$
   Корни уравнения:
   $x = \frac{11 \pm \sqrt{1}}{2} = \frac{11 \pm 1}{2}$
   $x_1 = 6$, $x_2 = 5$
   Меньший корень: 5
   Ответ: 5.
5. На клетчатой бумаге с размером клетки \(1\times1\) изображён ромб. Найдите площадь этого ромба.
   Решение: По рисунку определяем длины диагоналей:
   $d_1 = 6$ клеток, $d_2 = 8$ клеток
   Площадь ромба:
   $S = \frac{d_1 \cdot d_2}{2} = \frac{6 \cdot 8}{2} = 24$
   Ответ: 24.
6. В фирме такси в данный момент свободно 20 машин: 2 чёрных, 2 жёлтых и 16 зелёных. Найдите вероятность того, что к нему приедет жёлтое такси.
   Решение: Вероятность равна отношению количества жёлтых машин к общему числу:
   $P = \frac{2}{20} = 0,1$
   Ответ: 0,1.
7. Один из углов параллелограмма равен \(26^\circ\). Найдите большой угол этого параллелограмма.
   Решение: Сумма смежных углов параллелограмма равна $180^\circ$:
   Больший угол: $180^\circ - 26^\circ = 154^\circ$
   Ответ: 154.
8. Решите неравенство. В ответе укажите его наибольшее целое решение: \[ 3 - 2x \ge 8x - 1. \] Решение: Перенесём все слагаемые с $x$ влево:
   $3 + 1 \ge 8x + 2x$
   $4 \ge 10x$
   $x \le 0,4$
   Наибольшее целое решение: 0
   Ответ: 0.
9. Катет и гипотенуза прямоугольного треугольника равны 16 и 20. Найдите высоту, проведённую к гипотенузе.
   Решение: Найдём второй катет по теореме Пифагора:
   $b = \sqrt{20^2 - 16^2} = \sqrt{400 - 256} = \sqrt{144} = 12$
   Площадь треугольника:
   $S = \frac{16 \cdot 12}{2} = 96$
   Высота к гипотенузе:
   $h = \frac{2S}{c} = \frac{2 \cdot 96}{20} = 9,6$
   Ответ: 9,6.
10. Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 195 км — со скоростью 65 км/ч, а последние 225 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
    Решение: Общее расстояние:
    $S = 140 + 195 + 225 = 560$ км
    Общее время:
    $t = \frac{140}{70} + \frac{195}{65} + \frac{225}{75} = 2 + 3 + 3 = 8$ часов
    Средняя скорость:
    $v_{ср} = \frac{S}{t} = \frac{560}{8} = 70$ км/ч
    Ответ: 70.