Аничков Лицей из 9 в 10 класс 2010 год вариант 2

АНИЧКОВ ЛИЦЕЙ (СПБ)

2010 год

Вариант 2

1. Вычислить: \[ \frac{109^2 - 122\cdot109 + 61^2}{79^2 + 73^2 - 49^2 - 55^2}. \]
2. График функции \(y = ax^2 + bx + c\) пересекает ось ординат в точке \((0,-2)\), а его вершина находится в точке \((2,1)\). В каких точках этот график пересекает ось абсцисс?
3. Упростить выражение: \[ \Bigl(\frac{a^{1/2}+1}{a^{1/2}-1} +\frac{a^{1/2}-1}{a^{1/2}+1} -\frac{4}{a-1}\Bigr)^{-2}. \]
4. В параллелограмме две стороны и диагональ равны \(18\), \(24\) и \(30\). Найти высоты параллелограмма.
5. Построить график функции: \[ y = \frac{14x^2 + 29x + 2}{x + 2}. \] Принадлежит ли этому графику точка \((-2,-27)\)?
6. Один насос заполняет бассейн в 4 раза быстрее, чем второй. За какое время каждый из них, работая по отдельности, заполнит бассейн, если вместе они справляются за 8 часов?
7. Квадрат произведения двух чисел равен \(\tfrac14\), а их удвоенная сумма равна \(3\tfrac{4}{21}\). Составьте квадратное уравнение, корнями которого являются эти числа.
8. Периметр ромба равен 40 см, а одна из его диагоналей равна 12 см. Найти радиус окружности, вписанной в этот ромб.
9. Какой воздух тяжелее — влажный или сухой?
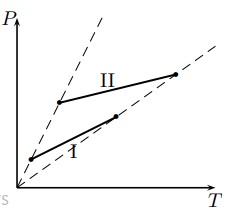
10. По графикам процессов (см. рисунок) определить, сжимался или расширялся газ во время нагревания. В каком из процессов изменение объёма было больше?
    

Решения задач

1. Вычислить: \[ \frac{109^2 - 122\cdot109 + 61^2}{79^2 + 73^2 - 49^2 - 55^2}. \] Решение: Преобразуем числитель как квадрат разности: \[ 109^2 - 122\cdot109 + 61^2 = (109 - 61)^2 = 48^2 = 2304. \] Знаменатель разложим на множители как разность квадратов: \[ 79^2 + 73^2 - 49^2 - 55^2 = (79 - 55)(79 + 55) + (73 - 49)(73 + 49) = 24 \cdot 134 + 24 \cdot 122 = 24 \cdot (134 + 122) = 24 \cdot 256 = 6144. \] Тогда выражение: \[ \frac{2304}{6144} = \frac{3}{8}. \] Ответ: $\frac{3}{8}$.
   
   
2. График функции \(y = ax^2 + bx + c\) пересекает ось ординат в точке \((0,-2)\), а его вершина находится в точке \((2,1)\). В каких точках этот график пересекает ось абсцисс?
   Решение: Из условия пересечения с осью ординат получаем \(c = -2\). Координаты вершины: \[ -\frac{b}{2a} = 2 \Rightarrow b = -4a. \] Подставив вершину \((2,1)\) в уравнение: \[ 1 = a \cdot 2^2 + b \cdot 2 - 2 \Rightarrow 1 = 4a + 2(-4a) - 2 \Rightarrow 1 = -4a - 2 \Rightarrow a = -\frac{3}{4}, \quad b = 3. \] Уравнение функции: \(y = -\frac{3}{4}x^2 + 3x - 2\). Для нахождения пересечений с осью абсцисс решим уравнение: \[ -\frac{3}{4}x^2 +3x -2 = 0 \Rightarrow 3x^2 -12x +8 = 0 \Rightarrow x = \frac{12 \pm \sqrt{48}}{6} = 2 \pm \frac{2\sqrt{3}}{3}. \] Ответ: \(\left(2 + \frac{2\sqrt{3}}{3}, 0\right)\), \(\left(2 - \frac{2\sqrt{3}}{3}, 0\right)\).
   
   
3. Упростить выражение: \[ \Bigl(\frac{a^{1/2}+1}{a^{1/2}-1} +\frac{a^{1/2}-1}{a^{1/2}+1} -\frac{4}{a-1}\Bigr)^{-2}. \] Решение: Пусть \(t = \sqrt{a}\). Преобразуем выражение: \[ \left(\frac{(t+1)^2 + (t-1)^2}{(t-1)(t+1)} - \frac{4}{t^2-1}\right)^{-2} = \left(\frac{2t^2 +2 -4}{t^2-1}\right)^{-2} = \left(\frac{2(t^2 -1)}{t^2-1}\right)^{-2} = 2^{-2} = \frac{1}{4}. \] Ответ: \(\frac{1}{4}\).
   
   
4. В параллелограмме две стороны и диагональ равны \(18\), \(24\) и \(30\). Найти высоты параллелограмма.
   Решение: По теореме о равенстве суммы квадратов сторон сумме квадратов диагоналей: \[ 2(18^2 + 24^2) = d_1^2 + d_2^2 \Rightarrow 2(324 + 576) = 900 + d_2^2 \Rightarrow d_2 = 30. \] Так как диагонали равны, параллелограмм является прямоугольником. Высоты равны сторонам: Ответ: \(18\) и \(24\).
   
   
5. Построить график функции: \[ y = \frac{14x^2 + 29x + 2}{x + 2}. \] Решение: Выполним деление числителя на знаменатель: \[ \frac{14x^2 +29x +2}{x + 2} = 14x +1 \quad \text{(остаток \(0\))}. \] Функция упрощается до прямой \(y =14x +1\) с исключением точки \(x =-2\). Проверим точку \((-2, -27)\): \[ y =14(-2)+1=-27, \] но \(x=-2\) приводит к делению на \(0\), поэтому точка не принадлежит графику. Ответ: График — прямая \(y=14x +1\) с выколотой точкой \((-2, -27)\). Нет, точка не принадлежит графику.
   
   
6. Один насос заполняет бассейн в 4 раза быстрее, чем второй. За какое время каждый из них, работая по отдельности, заполнит бассейн, если вместе они справляются за 8 часов?
   Решение: Пусть медленный насос заполняет бассейн за \(x\) часов, тогда быстрый за \(x/4\) часов. Совместная скорость: \[ \frac{1}{x} + \frac{4}{x} = \frac{5}{x} \Rightarrow x =5 \cdot8 =40. \] Ответ: \(10\) ч и \(40\) ч.
   
   
7. Квадрат произведения двух чисел равен \(\tfrac14\), а их удвоенная сумма равна \(3\tfrac{4}{21}\). Составьте квадратное уравнение, корнями которого являются эти числа.
   Решение: Пусть числа \(a\) и \(b\). Тогда: \[ (ab)^2 =\frac{1}{4} \Rightarrow ab =\pm\frac{1}{2}, \quad 2(a+b)=\frac{67}{21} \Rightarrow a+b=\frac{67}{42}. \] Составляя уравнение для каждого случая: \[ x^2 -\frac{67}{42}x +\frac{1}{2}=0 \quad \text{или} \quad x^2 -\frac{67}{42}x -\frac{1}{2}=0. \] Ответ: \(42x^2 -67x +21=0\) и \(42x^2 -67x -21=0\).
   
   
8. Периметр ромба равен 40,см, а одна из его диагоналей равна 12,см. Найти радиус окружности, вписанной в этот ромб.
   Решение: Сторона ромба \(40/4=10\),см. Из формулы диагоналей ромба: \[ 4 \cdot10^2 =12^2 +d_2^2 \Rightarrow d_2=16\,\text{см.} \] Площадь ромба: \[ \frac{1}{2} \cdot12\cdot16 =96\,\text{см}^2. \] Радиус вписанной окружности: \[ r =\frac{\text{Площадь}}{\text{Периметр}} =\frac{96}{40}=2,4\,\text{см.} \] Ответ: \(2,4\,\text{см}\).
   
   
9. Какой воздух тяжелее — влажный или сухой?
   Ответ: Сухой воздух тяжелее влажного, так как молекулы воды имеют меньшую молярную массу по сравнению с азотом и кислородом.
   
   
10. По графикам процессов (см. рисунок) определить, сжимался или расширялся газ во время нагревания. В каком из процессов изменение объёма было больше?
    Ответ: Нагревание при увеличении объёма соответствует расширению. Если на графике процесс показывает одновременное увеличение температуры и объёма — газ расширялся. Процесс с большим изменением объёма определяется по крутизне графика зависимости объёма от температуры (или площади под кривой на P-V диаграмме).