Аничков Лицей из 9 в 10 класс 2010 год вариант 1

АНИЧКОВ ЛИЦЕЙ (СПБ)

2010 год

Вариант 1

1. Вычислить: \[ \frac{53^2 + 22^2 - 47^2 - 16^2} {65^2 - 130\cdot59 + 59^2}. \]
2. График функции \(y=ax^2+bx+c\) пересекает ось \(OY\) в точке \((0,2)\), а его вершина находится в точке \((2,5)\). В каких точках этот график пересекает ось \(OX\)?
3. Упростить выражение: \[ \Bigl(\frac{x^{1/2}+2}{x^{1/2}-2} +\frac{x^{1/2}-2}{x^{1/2}+2} -\frac{16}{x-4}\Bigr)^{-2}. \]
4. В параллелограмме две стороны и диагональ равны \(21\), \(28\) и \(35\). Найти высоты параллелограмма.
5. Построить график функции: \[ y = \frac{16x^2 - 33x + 2}{x - 2}. \] Принадлежит ли этому графику точка \((2,31)\)?
6. Один насос заполняет бассейн в \(2\) раза быстрее, чем второй. За какое время каждый из насосов, работая отдельно, заполняет бассейн, если вместе они справляются за \(6\) часов?
7. Квадрат произведения двух чисел равен \(\tfrac14\), а их удвоенная сумма равна \(4\tfrac{1}{14}\). Составьте квадратное уравнение, корнями которого являются эти числа.
8. Периметр ромба равен \(52\) см, а одна из его диагоналей равна \(10\) см. Найти радиус окружности, вписанной в ромб.
9. В кабине космического корабля невесомость. Почему даже в невесомости существует давление воздуха?
10. Как изменялась температура идеального газа при процессах, графики которых изображены на рисунке ниже? Каким из этих процессов совершена большая работа и почему?
    

Решения задач

1. Вычислить: \[ \frac{53^2 + 22^2 - 47^2 - 16^2} {65^2 - 130\cdot59 + 59^2}. \]
   Решение: В числителе применим формулы разности квадратов:
   $(53^2 - 47^2) + (22^2 - 16^2) = (53 - 47)(53 + 47) + (22 - 16)(22 + 16) = 6 \cdot 100 + 6 \cdot 38 = 600 + 228 = 828$.
   В знаменателе распознаем квадрат разности:
   $65^2 - 130 \cdot 59 + 59^2 = (65 - 59)^2 = 6^2 = 36$.
   Итоговое значение: $\frac{828}{36} = 23$.
   Ответ: 23.
   
   
2. График функции \(y=ax^2+bx+c\) пересекает ось \(OY\) в точке \((0,2)\), а его вершина находится в точке \((2,5)\). В каких точках этот график пересекает ось \(OX\)?
   Решение: Коэффициент \(c = 2\). Координаты вершины:
   Дополним до формулы вершины: \(x_0 = -\frac{b}{2a} = 2 \quad \Rightarrow \quad b = -4a\).
   Подставим вершину в уравнение:
   $5 = a \cdot 2^2 + (-4a) \cdot 2 + 2 \quad \Rightarrow \quad 5 = 4a - 8a + 2 \quad \Rightarrow \quad -4a = 3 \quad \Rightarrow \quad a = -\frac{3}{4}$.
   Тогда \(b = -4 \cdot (-\frac{3}{4}) = 3\). Уравнение:
   $y = -\frac{3}{4}x^2 + 3x + 2$.
   Найдем пересечение с осью \(OX\):
   $-\frac{3}{4}x^2 + 3x + 2 = 0 \quad \Rightarrow \quad 3x^2 - 12x - 8 = 0$.
   Дискриминант: $D = 144 + 96 = 240 \quad \Rightarrow \quad x = \frac{12 \pm 4\sqrt{15}}{6} = 2 \pm \frac{2\sqrt{15}}{3}$.
   Ответ: $(2 + \frac{2\sqrt{15}}{3};0)$ и $(2 - \frac{2\sqrt{15}}{3};0)$.
   
   
3. Упростить выражение: \[ \Bigl(\frac{x^{1/2}+2}{x^{1/2}-2} +\frac{x^{1/2}-2}{x^{1/2}+2} -\frac{16}{x-4}\Bigr)^{-2}. \]
   Решение: Замена \(t = x^{1/2} \quad \Rightarrow \quad x = t^2\):
   $\left(\frac{t+2}{t-2} + \frac{t-2}{t+2} - \frac{16}{t^2-4}\right)^{-2}$.
   Общий знаменатель первых двух дробей \((t^2 - 4)\):
   $\frac{(t+2)^2 + (t-2)^2}{t^2 - 4} - \frac{16}{t^2 - 4} = \frac{2t^2 +8 -16}{t^2 -4} = \frac{2(t^2 -4)}{t^2 -4} = 2$.
   Возведем в \(-2\):
   \(2^{-2} = \frac{1}{4}\).
   Ответ: $\frac{1}{4}$.
   
   
4. В параллелограмме две стороны и диагональ равны \(21\), \(28\) и \(35\). Найти высоты параллелограмма.
   Решение: По формуле суммы квадратов сторон параллелограмма и диагонали:
   Диагональ \(35\) соответствует формуле: \(35^2 = 21^2 + 28^2 \quad \Rightarrow \quad 1225 = 441 + 784 \quad \Rightarrow \quad 1225 = 1225\).
   Значит, параллелограмм — прямоугольник. Площадь: \(21 \cdot 28 = 588\).
   Высоты равны сторонам:
   \(h_a = 21 \, \text{см}; \quad h_b = 28 \, \text{см}\).
   Ответ: 21 см и 28 см.
   
   
5. Построить график функции: \[ y = \frac{16x^2 - 33x + 2}{x - 2}. \] Принадлежит ли этому графику точка \((2,31)\)?
   Решение: Разложение числителя:
   Поделим числитель на \((x - 2)\):
   \((16x^2 -33x +2) : (x -2) = 16x -1\).
   Функция упрощается до \(y = 16x -1\) при \(x \neq 2\).
   Точка \((2,31)\) подстановкой дает значение \(31 = 16 \cdot 2 -1 = 31\), но функция не определена при \(x = 2\).
   Ответ: График прямой \(y =16x -1\) с выколотой точкой \(x=2\); точка \((2,31)\) не принадлежит.
   
   
6. Один насос заполняет бассейн в \(2\) раза быстрее, чем второй. За какое время каждый из насосов, работая отдельно, заполняет бассейн, если вместе они справляются за \(6\) часов?
   Решение: Пусть производительность первого насоса \(v\), тогда второго — \(\frac{v}{2}\).
   Совместная производительность: \(v + \frac{v}{2} = \frac{3v}{2}\).
   Время совместной работы: \(\frac{1}{\frac{3v}{2}} = \frac{2}{3v} = 6 \quad \Rightarrow \quad v = \frac{2}{18} = \frac{1}{9}\).
   Время первого: \(\frac{1}{v} = 9\) часов; второго: \(2 \cdot 9 = 18\) часов.
   Ответ: 9 часов и 18 часов.
   
   
7. Квадрат произведения двух чисел равен \(\tfrac14\), а их удвоенная сумма равна \(4\tfrac{1}{14}\). Составьте квадратное уравнение, корнями которого являются эти числа.
   Решение: Пусть числа \(a, b\):
   \((ab)^2 = \frac{1}{4} \quad \Rightarrow \quad ab = \pm \frac{1}{2}\).
   \(2(a + b) = \frac{57}{14} \quad \Rightarrow \quad a + b = \frac{57}{28}\).
   Квадратное уравнение: \(x^2 - \frac{57}{28}x \pm \frac{1}{2} = 0\).
   Умножим на 28: \(28x^2 - 57x \pm 14 = 0\). Проверка через сумму и произведение показывает правильность знака:
   Ответ для \(ab = \frac{1}{2}\): \(28x^2 -57x +14 = 0\).
   
   
8. Периметр ромба равен \(52\) см, а одна из его диагоналей равна \(10\) см. Найти радиус окружности, вписанной в ромб.
   Решение: Сторона ромба: \(52 \, \text{см} / 4 = 13 \, \text{см}\).
   Диагонали: \(d_1 =10 \, \text{см}\), \(d_2 = \sqrt{4 \cdot13^2 -10^2} = 24 \, \text{см}\).
   Площадь: \(\frac{10 \cdot24}{2} =120 \, \text{см}^2\).
   Радиус вписанной окружности: \(r = \frac{S}{p} = \frac{120}{26} = \frac{60}{13} \, \text{см}\).
   Ответ: \(\frac{60}{13} \, \text{см}\).
   
   
9. В кабине космического корабля невесомость. Почему даже в невесомости существует давление воздуха?
   Ответ: Давление создается ударами молекул газа о стенки кабины. Невесомость не влияет на тепловое движение молекул, поэтому давление сохраняется.
   
   
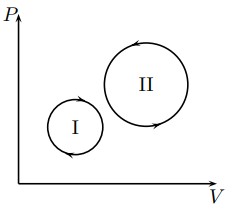
10. Как изменялась температура идеального газа при процессах, графики которых изображены на рисунке ниже? Каким из этих процессов совершена большая работа и почему?
    
    Решение (гипотетическое):
    На графике изображены процессы изотермического расширения (\(P\) уменьшается при увеличении \(V\)) и изобарного нагревания (\(V\) увеличивается с нагревом). Большая работа совершена процессом с большей площадью под кривой в \(P-V\) диаграмме (например, изобарным при большем изменении объема).