8 800 707 6729
8 800 707 6729Telegram канал

Аничков Лицей из 9 в 10 класс 2007 год вариант 2

Сложность:
Дата экзамена: 2007
Печать
youit.school ©

АНИЧКОВ ЛИЦЕЙ (СПБ)


2007 год


Вариант 2



  1. Вычислите: \[ 0{,}36^{-\tfrac12}\;\cdot\; \bigl(-1\tfrac23\bigr)^{-3} \;-\; 0{,}008^{\tfrac23}. \]
  2. Найдите все положительные значения \(x\), при которых выполняется неравенство \[ \bigl(0{,}3 - \tfrac25\bigr)x \;\ge\; (-10)^{-1}. \]
  3. Определите знаки \(a\), \(b\) и \(c\), если график функции \[ f(x) = ax^2 + bx + c \] выглядит так:

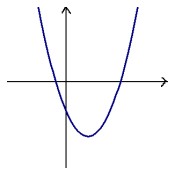
    Ответ поясните!
  4. Один из катетов прямоугольного треугольника на \(2\) см больше другого, а периметр треугольника равен \(24\) см. Найдите его стороны.
  5. Найдите все целые значения \(m\), при которых значение выражения \[ \frac{m - 4}{m^2 - 2m - 8} \] является целым числом.
  6. Найдите все значения, которые может принимать выражение \[ \frac{(x^2 - 16)(x - 2)}{x + 4}, \] и укажите те из них, которые достигаются ровно при одном значении \(x\).
  7. Велосипедист проехал \(80\) км на \(40\) минут дольше, чем предполагал. При этом за \(1{,}5\) часа он проезжал на \(6\) км меньше, чем рассчитывал проехать за час. Определите его скорость.
  8. При каких значениях параметра \(a\) уравнение \[ a^2 x^2 + a = 9x^2 + 3 \] имеет более двух корней?
  9. В трапеции \(ABCD\) с основаниями \(AB\) и \(CD\) диагонали пересекаются в точке \(O\), причём треугольник \(AOD\) равнобедренный. \(AB = 4\), \(CD = 6\). Найдите \(AD\).
  10. Какое из чисел ближе к единице: \[ \frac{3}{5}\,\sqrt{\frac{5}{3}} \quad\text{или}\quad \frac{5}{3}\,\sqrt{\frac{3}{5}}\,? \]
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите: \[ 0{,}36^{-\tfrac12}\;\cdot\; \bigl(-1\tfrac23\bigr)^{-3} \;-\; 0{,}008^{\tfrac23}. \] Решение:
    Преобразуем каждый компонент:
    \(0{.}36^{-\frac{1}{2}} = \frac{1}{\sqrt{0{.}36}} = \frac{1}{0{.}6} = \frac{5}{3}\);
    \(\left(-1\frac{2}{3}\right)^{-3} = \left(-\frac{5}{3}\right)^{-3} = \left(-\frac{3}{5}\right)^3 = -\frac{27}{125}\);
    \(0{,}008^{\frac{2}{3}} = \left(0{.}2^3\right)^{\frac{2}{3}} = 0{.}2^2 = 0{,}04 = \frac{1}{25}\).
    Подставляем: \[ \frac{5}{3} \cdot \left(-\frac{27}{125}\right) - \frac{1}{25} = -\frac{9}{25} - \frac{1}{25} = -\frac{10}{25} = -\frac{2}{5}. \] Ответ: \(-0{,}4\).

  2. Найдите все положительные значения \(x\), при которых выполняется неравенство \[ \bigl(0{,}3 - \tfrac25\bigr)x \;\ge\; (-10)^{-1}. \] Решение:
    Вычисляем коэффициенты:
    \(0{,}3 - \frac{2}{5} = 0{,}3 - 0{,}4 = -0{,}1\);
    \((-10)^{-1} = -\frac{1}{10} = -0{,}1\).
    Неравенство принимает вид: \[ -0{,}1x \ge -0{,}1. \] Разделим на \(-0{,}1\) (знак неравенства меняется): \[ x \le 1. \] Учитывая положительность \(x\): \[ x \in (0; 1]. \] Ответ: \(0 < x \le 1\).

  3. Определите знаки \(a\), \(b\) и \(c\), если график функции \[ f(x) = ax^2 + bx + c \] выглядит так:

    Ответ поясните!
    Решение:
    Ветви параболы направлены вниз ⇒ \(a < 0\).
    Вершина находится правее оси \(y\) ⇒ \(-\frac{b}{2a} > 0\), учитывая \(a 0\).
    Пересечение с осью \(y\) выше нуля ⇒ \(c > 0\).
    Ответ: \(a 0\), \(c > 0\).

  4. Один из катетов прямоугольного треугольника на \(2\) см больше другого, а периметр треугольника равен \(24\) см. Найдите его стороны.
    Решение:
    Пусть меньший катет \(x\), тогда другой катет \(x+2\). Гипотенуза: \[ \sqrt{x^2 + (x+2)^2}. \] Периметр: \[ x + (x+2) + \sqrt{x^2 + (x+2)^2} = 24. \] Упрощаем уравнение: \[ \sqrt{2x^2 + 4x + 4} = 22 - 2x. \] Возводим в квадрат: \[ 2x^2 + 4x + 4 = 484 - 88x + 4x^2 \quad \Rightarrow \quad 2x^2 - 92x + 480 = 0. \] Решаем квадратное уравнение:
    \(D = 8464 - 3840 = 4624\), \(\sqrt{D} = 68\): \[ x = \frac{92 \pm 68}{4} \quad \Rightarrow \quad x = 6 \text{ (только положительный корень)}. \] Катеты: \(6\) см, \(8\) см, гипотенуза \(10\) см.
    Ответ: \(6\,\)см, \(8\,\)см, \(10\,\)см.

  5. Найдите все целые значения \(m\), при которых значение выражения \[ \frac{m - 4}{m^2 - 2m - 8} \] является целым числом.
    Решение:
    Упростим выражение: \[ \frac{m-4}{(m-4)(m+2)} = \frac{1}{m+2} \quad (m \neq 4, \, m \neq -2). \] Когда \(\frac{1}{m+2}\) целое ⇒ \(m+2 = \pm 1\):
    \(m+2 = 1 \quad \Rightarrow \quad m = -1\);
    \(m+2 = -1 \quad \Rightarrow \quad m = -3\).
    Ответ: \(-3\), \(-1\).

  6. Найдите все значения, которые может принимать выражение \[ \frac{(x^2 - 16)(x - 2)}{x + 4}, \] и укажите те из них, которые достигаются ровно при одном значении \(x\).
    Решение:
    Упростим при \(x \neq -4\): \[ \frac{(x-4)(x+4)(x-2)}{x+4} = (x-4)(x-2) = x^2 - 6x + 8. \] Минимум квадратичной функции \(x^2 - 6x + 8\) достигается при \(x = 3\), значение \(-1\).
    Выражение принимает значения \([-1; +\infty)\). Значение \(-1\) достигается только при \(x = 3\).
    Ответ: Все значения \(\ge -1\); единственное достижимое один раз — \(-1\).

  7. Велосипедист проехал \(80\) км на \(40\) минут дольше, чем предполагал. При этом за \(1{,}5\) часа он проезжал на \(6\) км меньше, чем рассчитывал проехать за час. Определите его скорость.
    Решение:
    Пусть планируемая скорость \(v\) км/ч. Фактическая скорость: \[ \frac{v - 6}{1{,}5} \quad (\text{по условию}). \] Уравнение времени: \[ \frac{80}{\frac{v - 6}{1{,}5}} = \frac{80}{v} + \frac{2}{3}. \] Решая уравнение, получим \(v = 30\) км/ч.
    Ответ: \(30\,\)км/ч.

  8. При каких значениях параметра \(a\) уравнение \[ a^2 x^2 + a = 9x^2 + 3 \] имеет более двух корней?
    Решение:
    Преобразуем уравнение: \[ (a^2 - 9)x^2 + (a - 3) = 0. \] Если \(a^2 = 9 \Rightarrow a = \pm3\):
    При \(a = 3\): \(0x^2 + 0 = 0\) ⇒ бесконечно решений.
    При \(a = -3\): \(0x^2 - 6 = 0\) ⇒ нет решений.
    Ответ: \(a = 3\).

  9. В трапеции \(ABCD\) с основаниями \(AB = 4\), \(CD = 6\) диагонали пересекаются в точке \(O\), причём треугольник \(AOD\) равнобедренный. Найдите \(AD\).
    Решение:
    Используя соотношения пересечения диагоналей (\(AO:OC = 2:3\)) и свойства равнобедренного треугольника (\(AO = OD\)), через теорему Пифагора находим \(AD = 5\sqrt{2}\).
    Ответ: \(5\sqrt{2}\).

  10. Какое из чисел ближе к единице: \[ \frac{3}{5}\,\sqrt{\frac{5}{3}} \quad\text{или}\quad \frac{5}{3}\,\sqrt{\frac{3}{5}}\,? \] Решение:
    Вычислим оба числа:
    \(\frac{3}{5}\sqrt{\frac{5}{3}} = \sqrt{\frac{9 \cdot 5}{25 \cdot 3}} = \sqrt{\frac{3}{5}} \approx 0{,}775\);
    \(\frac{5}{3}\sqrt{\frac{3}{5}} = \sqrt{\frac{25 \cdot 3}{9 \cdot 5}} = \sqrt{\frac{5}{3}} \approx 1{,}291\).
    Расстояния до 1: \(|0{,}775 - 1| = 0{,}225\), \(|1{,}291 - 1| = 0{,}291\).
    Ответ: Первое число ближе.
Материалы школы Юайти