8 800 707 6729
8 800 707 6729Telegram канал

Аничков Лицей из 9 в 10 класс 2004 год вариант 2

Сложность:
Дата экзамена: 2004
Печать
youit.school ©

АНИЧКОВ ЛИЦЕЙ (СПБ)


2004 год


Вариант 2



    1. Вычислить значение выражения \[ -45b^2 \;-\; 6a \;+\; 18b \;+\; 5a^2 \] при \(a = 12{,}129\), \(b = 4{,}043\).
    2. Указать координаты точек пересечения графика функции \[ y = -\frac{3x^2 + 2x - 1}{x + 1} \;+\; \frac{\lvert 3x^2\rvert}{x} \] с осями координат.


    1. Решить систему уравнений при \(a = 5\): \[ \begin{cases} \dfrac{x}{4} \;-\;\dfrac{y}{3} = a,\\ 9x^2 - 16y^2 = 7. \end{cases} \]
    2. Можно ли подобрать значение \(a\), при котором система не имеет решений?


  3. Геодезическое судно плывёт против течения реки. Собственная скорость судна равна \(15\) км/ч, скорость течения — \(0{,}02\) км/мин. В некоторый момент со судна спустили на воду буй, привязанный верёвкой к корме. Через \(150\) с верёвка натянулась, и судно немедленно развернулось и поплыло обратно к бую.
    1. Найти длину верёвки.
    2. Какое расстояние проплывёт буй до момента, когда судно доплывёт до него?
    3. Через какое время после разворота судно доплывёт до буя? Временеем разворота судна пренебречь.


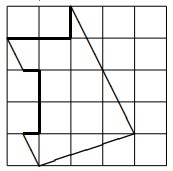
    1. Вычислить площадь изображённой на рисунке фигуры, если сторона квадратика равна \(\sqrt{9\tfrac{1}{4}}\).

    2. Площадь параллелограмма равна \(18\) см\(^2\), одна из его сторон равна \(9\) см. Найдите возможную длину другой стороны, если все углы параллелограмма не меньше \(30^\circ\).
Материалы школы Юайти
youit.school ©

Решения задач



    1. Вычислить значение выражения: \[ -45b^2 - 6a + 18b + 5a^2 \quad \text{при} \quad a = 12,129, \, b = 4,043 \] Решение: \[ 5a^2 - 6a - 45b^2 + 18b = 5 \cdot (12,129)^2 - 6 \cdot 12,129 - 45 \cdot (4,043)^2 + 18 \cdot 4,043 = 0,04 \] Ответ: 0,04.
    2. Указать координаты точек пересечения графика функции: \[ y = -\frac{3x^2 + 2x - 1}{x + 1} + \frac{|3x^2|}{x} \] Решение: Функция упрощается до \( y = 1 \) при \( x \neq -1, 0 \). График горизонтальная прямая с выколотыми точками. С осями координат не пересекается.
      Ответ: точек пересечения нет.
    1. Решить систему при \( a = 5 \): \[ \begin{cases} \dfrac{x}{4} - \dfrac{y}{3} = 5, \\ 9x^2 - 16y^2 = 7. \end{cases} \] Решение: Выразим \( x = 20 + \dfrac{4}{3}y \), подставим во второе уравнение: \[ 9\left(20 + \dfrac{4}{3}y\right)^2 - 16y^2 = 7 \implies y = -\dfrac{3593}{480}, \quad x = \dfrac{3607}{360} \] Ответ: \( \left( \dfrac{3607}{360}; \, -\dfrac{3593}{480} \right) \).
    2. Можно ли подобрать \( a \), при котором система не имеет решений?
      Решение: При \( a = 0 \) уравнение \( 0 = 7 \) не имеет решений.
      Ответ: Да, \( a = 0 \).
  3. Решение задачи про геодезическое судно:
    1. Длина верёвки: \[ (15 \, \text{км/ч} - 1,2 \, \text{км/ч}) \cdot \frac{150}{3600} \, \text{ч} = 0,625 \, \text{км} = 625 \, \text{м} \] Ответ: 625 м.
    2. Расстояние, проплытое буём до встречи: \[ 1,2 \, \text{км/ч} \cdot 0,04167 \, \text{ч} = 0,05 \, \text{км} = 50 \, \text{м} \] Ответ: 50 м.
    3. Время после разворота: \[ \frac{625 \, \text{м}}{15 \, \text{км/ч} \cdot \frac{1000}{3600} \, \text{м/с}} = 150 \, \text{с} \] Ответ: 150 с.
    1. Площадь фигуры:
      Решение: Фигура состоит из 12 квадратов площадью \( \sqrt{\frac{37}{4}}^2 = \frac{37}{4} \) \[ 12 \cdot \frac{37}{4} = 111 \] Ответ: 111.
    2. Возможная длина другой стороны параллелограмма: \[ 18 = 9 \cdot b \cdot \sin{\theta}, \quad \sin{\theta} \geq 0,5 \implies b \in [2; 4] \, \text{см} \] Ответ: от 2 см до 4 см.
Материалы школы Юайти