Школа №57 из 10 в 11 класс 2022 год вариант 1

ШКОЛА №57

2022 год

Вариант 1

1. Из двух пунктов, расстояние между которыми 100 м, одновременно навстречу друг другу начали двигаться два тела. Скорость одного из них 20 м/с. Какова скорость второго тела, если оба тела встретились через 4 с?
   
   
2. Пешеход часть пути прошёл со скоростью 3 км/ч, затратив на это $\tfrac23$ времени своего движения. За оставшуюся треть времени он прошёл остальной путь со скоростью 6 км/ч. Определите среднюю скорость движения пешехода.
   
   
3. Какова плотность сплава из 300 г олова и 100 г свинца? Плотность олова 7300 кг/м³, плотность свинца 11300 кг/м³.
   
   
4. Чему равен вес полого медного куба с длиной ребра 7 см и толщиной стенок 1 см? Плотность меди равна 8900 кг/м³.
   
   
5. Три жидкости имеют плотности $\rho$, $2\rho$ и $3\rho$. В первом опыте юные физики смешали равные объёмы этих жидкостей. Получилась жидкость плотности $\rho_1$. Во втором опыте смешали равные массы этих жидкостей. Получилась жидкость плотности $\rho_2$. Найти отношение $\rho_1 / \rho_2$.
   
   
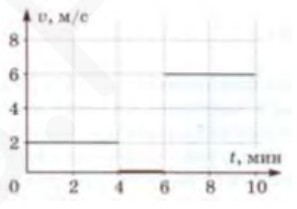
6. На графике приведена зависимость скорости пешехода от времени его движения. Постройте график зависимости скорости этого пешехода от пройденного им расстояния.
   
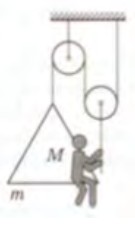
7. Мальчик соорудил себе подвесное кресло и с его помощью приподнял себя над землёй. С какой силой мальчик должен тянуть верёвку, и с какой силой он давит на сиденье, если масса мальчика $M=50\,$кг, а масса кресла $m=20\,$кг?
   
   
   

Решения задач

1. Из двух пунктов, расстояние между которыми 100 м, одновременно навстречу друг другу начали двигаться два тела. Скорость одного из них 20 м/с. Какова скорость второго тела, если оба тела встретились через 4 с?
   Решение: Путь, пройденный первым телом за 4 секунды:
   $S_1 = v_1 \cdot t = 20 \cdot 4 = 80$ (м).
   Тогда путь второго тела:
   $S_2 = 100 - 80 = 20$ (м).
   Скорость второго тела:
   $v_2 = \frac{S_2}{t} = \frac{20}{4} = 5$ (м/с).
   Ответ: 5 м/с.
2. Пешеход часть пути прошёл со скоростью 3 км/ч, затратив на это $\tfrac23$ времени своего движения. За оставшуюся треть времени он прошёл остальной путь со скоростью 6 км/ч. Определите среднюю скорость движения пешехода.
   Решение: Пусть общее время движения $t$. Тогда:
   Путь за $\tfrac{2}{3}t$:
   $S_1 = 3 \cdot \tfrac{2}{3}t = 2t$ (км).
   Путь за $\tfrac{1}{3}t$:
   $S_2 = 6 \cdot \tfrac{1}{3}t = 2t$ (км).
   Средняя скорость:
   $v_{\text{ср}} = \frac{S_1 + S_2}{t} = \frac{2t + 2t}{t} = 4$ (км/ч).
   Ответ: 4 км/ч.
3. Какова плотность сплава из 300 г олова и 100 г свинца? Плотность олова 7300 кг/м³, плотность свинца 11300 кг/м³.
   Решение: Общая масса сплава:
   $m = 300 + 100 = 400$ г $= 0,4$ кг.
   Объём сплава:
   $V = \frac{0,3}{7300} + \frac{0,1}{11300} \approx 0,00004995$ м³.
   Плотность:
   $\rho = \frac{m}{V} = \frac{0,4}{0,00004995} \approx 8008$ кг/м³ $\approx 8000$ кг/м³.
   Ответ: 8000 кг/м³.
4. Чему равен вес полого медного куба с длиной ребра 7 см и толщиной стенок 1 см? Плотность меди равна 8900 кг/м³.
   Решение: Внутренний объём куба:
   $V_{\text{внут}} = (7 - 2 \cdot 1)^3 = 5^3 = 125$ см³.
   Объём меди:
   $V_{\text{меди}} = 7^3 - 5^3 = 218$ см³ $= 0,000218$ м³.
   Масса куба:
   $m = 8900 \cdot 0,000218 \approx 1,94$ кг.
   Вес:
   $P = m \cdot g \approx 1,94 \cdot 10 \approx 19,4$ Н.
   Ответ: 19,4 Н.
5. Три жидкости имеют плотности $\rho$, $2\rho$ и $3\rho$. В первом опыте смешали равные объёмы, во втором — равные массы. Найдите отношение $\rho_1 / \rho_2$.
   Решение: Для равных объёмов $(V)$:
   $\rho_1 = \frac{V\rho + V \cdot 2\rho + V \cdot 3\rho}{3V} = 2\rho$.
   Для равных масс $(m)$:
   Общий объём: $V_{\text{общ}} = \frac{m}{\rho} + \frac{m}{2\rho} + \frac{m}{3\rho} = \frac{11m}{6\rho}$.
   $\rho_2 = \frac{3m}{\frac{11m}{6\rho}} = \frac{18\rho}{11}$.
   Отношение:
   $\frac{\rho_1}{\rho_2} = \frac{2\rho}{\frac{18\rho}{11}} = \frac{11}{9}$.
   Ответ: $\frac{11}{9}$.
6. Постройте график зависимости скорости пешехода от пройденного расстояния.
   График состоит из трёх участков:
   • От 0 до 10 м: скорость равномерно возрастает от 0 до 2 м/с.
   • От 10 до 50 м: постоянная скорость 2 м/с.
   • От 50 до 70 м: скорость равномерно снижается от 2 до 0 м/с.
   
   Ответ: График построен.
7. Мальчик массой 50 кг и кресло массой 20 кг подвешены с помощью системы блоков. Сила натяжения верёвки и сила давления на сиденье:
   Решение: Общий вес системы:
   $(50 + 20) \cdot 10 = 700$ Н.
   Сила натяжения верёвки:
   $T = \frac{700}{2} = 350$ Н.
   Сила давления на сиденье:
   $N = 50 \cdot 10 - 350 = 150$ Н.
   Ответ: Сила тяги — 350 Н, сила давления — 150 Н.