Абстрактное мышление: как помочь ребёнку мыслить шире

Абстрактное мышление: как помочь ребёнку мыслить шире

Представьте: ребёнок читает задачу про Петю, который идёт в магазин за мороженым, а в голове уже видит «объект движется со скоростью X». Это и есть абстрактное мышление — умение выходить за рамки конкретики и видеть суть.

Что это и зачем нужно?

Абстрактное мышление — это способность превращать сложные концепции в понятные образы. Оно позволяет ребёнку видеть за конкретными числами и условиями задач глубокие закономерности — именно так рождаются решения олимпиадных задач, где важно не вычисление, а идея.

Абстрактное мышление лучше помогает усваивать высшую математику, ведь она перестаёт быть набором формул, а становится системой взаимосвязанных концепций. Это вместо заучивания дороги к дому ребёнок учится свободно ориентироваться по карте в любом незнакомом месте.

Где пригодится абстрактное мышление?

• В олимпиадах: задачи, где важнее модель, чем вычисления
• В программировании: умение видеть алгоритм за конкретным кодом
• В жизни: анализировать ситуации, а не действовать шаблонно

Как оно развивается?

У детей этот навык растёт постепенно:

• 4-5 класс: учатся удерживать в голове условие и образы
• 6-7 класс: переходят от конкретного «Пети» к «объекту», пробуют мысленные эксперименты
• Старшая школа: свободно работают с абстракциями в физике, геометрии, программировании

Такое разделение, конечно же, условно — все дети развиваются по-своему, но тренировать абстрактное мышление можно уже с начальной школы (или даже раньше, если видите интерес!)

Как развивать?

1. Визуализировать
Просите ребёнка рисовать условие задачи: «Изобрази, как Петя идёт в магазин. Где тут расстояние, время, скорость?»

Пользу такого подхода подтверждают и учёные: согласно исследованию в Journal of Educational Psychology (2018), дети, которые рисуют условия задач, на 23% лучше справляются с абстрактными заданиями.

2. Развивать логику
Предлагайте ребёнку задачи без чисел, на логику.

«Если все коты — животные, а Барсик — кот, то кто Барсик?». Учимся видеть структуру, а не цифры.

3. Придумывать свои задачи

Добавьте немножко куража в занятия математикой и попросите ребёнка придумывать свои задачи. Сначала — простые, потом — чуть сложнее.

Составь задачу про то, как Маша делит яблоки, но чтобы в ней была скрыта формула.

4. Кстати, дети, регулярно играющие в стратегические игры, улучшают свои когнитивные способности на 15-20%, что подтверждает мета-анализ научных исследований 2020 года.

Скорее доставайте стратегические настолки, шахматы, и даже компьютерные стратегии — всё это пойдёт на пользу!

Что дать ребёнку для тренировки?

• Учебники: Петерсон (отличные визуальные задачи), «Наглядная геометрия»
• Олимпиады: «Кенгуру», «КИТ» — много нестандартных заданий
• Платформы: problems.ru — база задач с разбором

Примеры задач

Судоку. 4 класс

Многие игры, как, например, судоку, отлично развивают!

Основная сложность подобных игр в том, что ученик сталкивается с неполными данными, что, в свою очередь, заставляет анализировать и планировать

В процессе решения приходится представлять различные варианты развития событий и просчитывать последствия своих действий – это ключевой аспект развития абстрактного мышления

Шахматная задача. 4 класс

Расставьте на шахматной доске 32 коня так, чтобы каждый бил ровно два других.

Шахматные задачи неизменно хорошо прокачивают абстрактное мышление.
Этому способствует огромное количество воозможных комбинаций, которые нужно представить и удержать в голове

Фигуры часто взаимодействуют друг с другом и это взаимодействие меняется в зависимости от положения и их количества. Таким образом даже для двух фигур мозг анализирует комплексную задачу: необходимо отслеживать положение нескольких фигур + их взаимодействие друг с другом

Графы. 5 класс

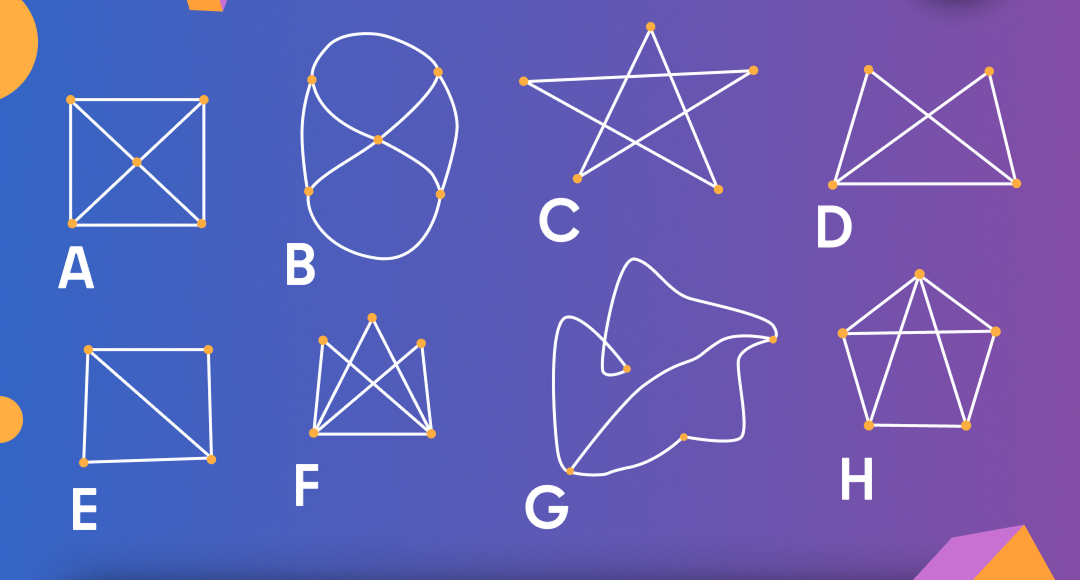
Найдите все одинаковые графы на картинке.

Задачи на графы, в частности на их изоморфизм, отлично прокачивают мышление:

• Графы сами по себе являются довольно абстрактной структурой и часто несут широкую вариативность;
• Они отлично учат строить, видеть и следить за связями между объектами;
• Задачи по изоморфизму направлены как раз на этот навык – отслеживать связи и находить смысловую аналогию в противовес визуальному несовпадению.

Геометрическая задача на поворот. 6 класс

На какой наименьший угол нужно повернуть правильный шестиугольник вокруг точки пересечения его диагоналей, чтобы он совместился сам с собой?

Задача несложная и, разбив её на этапы, можно увидеть следующие идеи:

• Ученик должен представлять в голове, как работает поворот фигуры;
• Нужно определить, вокруг какой точки происходит поворот и как это влияет на движение;
• Представив картину в голове, необходимо зафиксировать момент наложения одной фигуры на другую.

Дальше идёт техническая часть, однако всё ещё нужно понять, какую часть полного круга задействует поворот фигуры и как это вычислить.

Геометрическая задача на траекторию. 7 класс

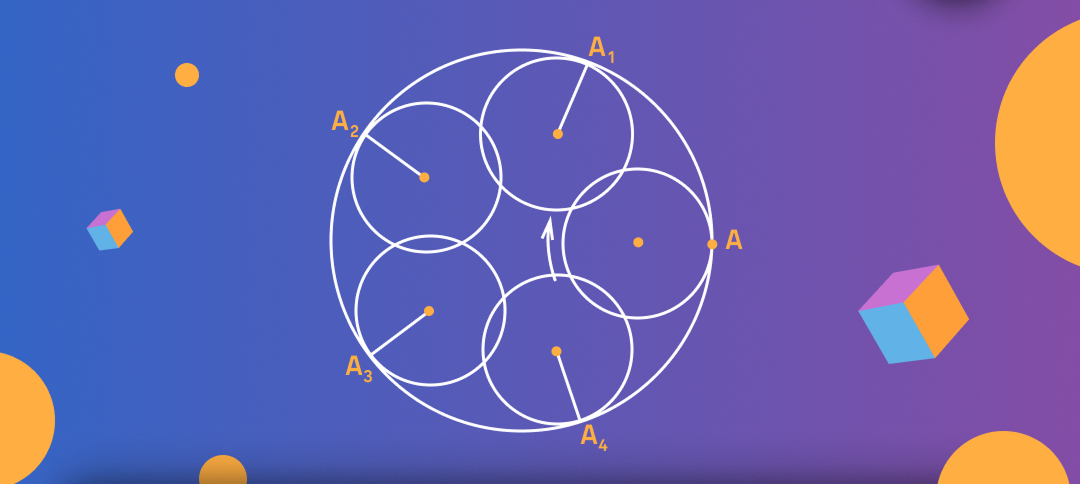
Изобразите траекторию движения вокруг точки, закрепленной на окружности, катящейся внутри другой окружности в 2,5 раза большего радиуса. (Воспользуйтесь тем, что длина маленькой окружности в 2.5 раза меньше длины большой окружности)

Задача уже на порядок сложнее:

• Необходимо представить сложное одновременное движение нескольких фигур сразу;
• Объять в голове движение всех фигур разом трудно, поэтому далее логичным шагом будет декомпозиция на этапы;
• Столкнувшись с трудностью, ученик может начать искать пути упрощения, например, сначала представить движение большого круга, а маленькие оставить неподвижными

Справившись с этим этапом, можно добавлять движение малых кругов и продолжать следить за траекторией — визуальное мышление здесь задействуется очень сильно

Геометрическая задача на траекторию. 8 класс

Жук ползёт по рёбрам
а) тетраэдра (на рисунке слева)
в) куба
с) октаэдра (на рисунке справа)

Сможет ли он последовательно обойти все рёбра, проходя по каждому ровно один раз?

Логичным усложнением классической геометрии будут объёмные фигуры:

• Необходимо вообразить движение в пространстве;
• Здесь неизменно будет возникать задача вращения объёмной фигуры, построение траектории в пространстве.

Главное правило: не заставлять, а увлекать.

Покажите, как абстракции превращают сложное в простое — и ребёнок сам захочет мыслить глубже!