Разбор школьного этапа ВСОШ по программированию 2025

Календарь основных олимпиадных событий!
Планируем на два шага вперёд.

Даты этапов и периоды проведения

От методистов Юайти

Вчера, 21 октября 2025 в Москве прошёл школьный этап ВсОШ по программированию.

Поспешили подготовить разбор задач для ребят! Передаём слово основателю школы – Матвею Грицаеву.

Школьный этап Всеросса 2025–2026 оказался довольно классическим.
Не слишком простым, не слишком сложным, всё по канону: две задачи на математику и формулы, НОД/НОК, немного конструктивов и жадность с элементами C++.

Единственное, что выбивалось: последняя задача.
Она была заметно сложнее обычного для школьного этапа и требовала уже продвинутого владения C++, что раньше встречалось разве что на региональном уровне.

В остальном — отличный набор задач.
Многие ребята, как и обычно, потеряли баллы и время на мелких подводных камнях, но для сильных участников этот тур стал хорошей разминкой перед сезоном олимпиад.
Для них цель была очевидна: 500 из 500.

Если соотнести уровень с нашими курсами:

Чтобы набрать около 460 баллов, достаточно знаний уровня Алгоритмы lvl 1 + ОлПрактика lvl 2;
Чтобы взять 500/500, нужен уровень Алгоритмы lvl 3 или C++ Pro + ОлПрактика lvl 4–5.

Отдельно отмечу последнюю задачу: она использовала тему, редкую для школьного и муниципального этапов, чаще встречающуюся на региональном или заключительном турах.
Видно, что уровень ребят растёт, и организаторы постепенно усложняют подборку.

Небольшие претензии остались к задаче C.
По отзывам и присланным решениям, некоторые работы, получившие 100 баллов, были некорректны, у меня даже есть антитесты, которые не были включены в проверку.
Надеюсь, в будущем авторы внимательнее проверят подобные случаи.

А теперь перейдём к разбору задач…

Задача А. Рекламная пауза

Краткий пересказ условия задачи:

Фильм длится n минут (без рекламы).
Каждые a минут вставляется рекламный блок длиной b минут.

Если момент начала рекламы совпадает с концом фильма, то рекламу не показывают.
Нужно найти общее время показа вместе с рекламой.

Темы:

Формулы
Математика
Условный оператор

(уровень Python Start + ОлПрактика lvl 1)

Ключевая идея

Нужно посчитать, сколько раз вставится реклама.
Реклама появляется после каждых a минут:
после a, 2a, 3a, … и так далее.

Если фильм длится ровно n, и это кратно a, то последняя реклама не вставляется, ведь фильм уже закончился.

Пример

Фильм длится 12 минут, реклама каждые 3 минуты.
Рекламные вставки будут после 3, 6, 9 минут, но не после 12.

Если же фильм длится 13 минут, то последняя реклама (на 12-й минуте) появится.

Это удобно учесть формулой:

if n % a == 0:
    reklama = n // a - 1
else:
    reklaman = n // a 
# можно проще формулой reklama = (n - 1) // a

Дальше остаётся соединить действия:

a, b, n = int(input()), int(input()), int(input())
reklama = (n - 1) // a
print(n + b * reklama)

Задача B. Популярный пост

Краткий пересказ условия задачи:

В мессенджере «Дружба» под сообщением оставили реакции трёх типов:

«Согласен» — $a$ штук,
«Не согласен» — $b$ штук,
«Забавно» — $c$ штук.

Каждый пользователь может поставить не больше двух разных реакций.
Нужно найти минимальное количество пользователей, которые могли это сделать.

Темы:

Формулы
Математика
Условный оператор
Конструктивные рассуждения
Жадные идеи

(уровень Python Start + ОлПрактика lvl 1)

Ключевая идея:

Каждый пользователь может поставить не больше двух разных реакций.
Значит, всего реакций: $s = a + b + c$

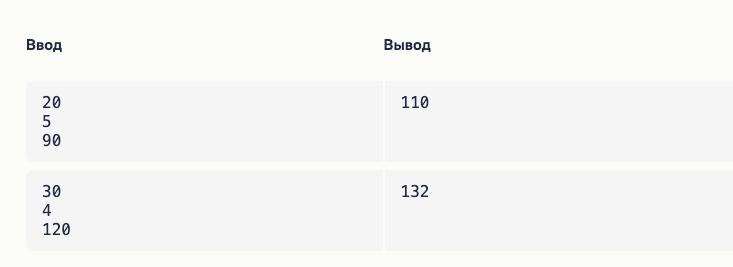
Тогда пользователей не могло быть меньше, чем $s / 2$ с округлением в большую сторону. То есть 19 реакций могли оставить 10 человек минимум.

А ещё пользователей не может быть меньше, чем реакций какого-то типа. То есть, если реакций «Согласен» — 13, то и людей от 13 и выше. И оба ограничения должны выполняться одновременно, поэтому берём максимум из них:

a, b, c = int(input()), int(input()), int(input())
s = a + b + c
ans = max((s + 1) // 2, a, b, c)
# тут аналогично первому номеру, если добавить к числу 1 и 
# потом поделить на 2, то это равноценно округлению вверх

На олимпиаде не требуется доказывать факт, поэтому мы можем выйти на идею через частные случаи.

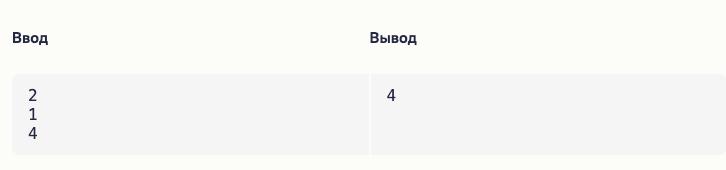
Можно было просто перебрать разные варианты: (2, 1, 4), (3, 2, 1), (10, 2, 0), (10, 4, 5) и через жадность понять закономерность.

Главная идея: нужно брать самую частую реакцию и постепенно «снимать» её вместе со второй по популярности.
Например, если реакции (10, 4, 5), то последовательность изменений могла быть такой:
→ (9, 4, 4)
→ (8, 4, 3)
→ (7, 3, 3)
→ (6, 3, 2)
→ (5, 2, 2)
и так далее — пока не станет очевидно, как работает принцип.

Многие ребята, к сожалению, застряли именно на этой задаче.
Те, кто могли спокойно выйти на 400+ баллов, не смогли вовремя отпустить идею добить её на 100 и потеряли на этом от 70 до 200 баллов в итоге.

Задача С. Встреча у фонтана

Короткое условие

Маша идёт до фонтана m минут, Паша — p минут.
Они выходят одновременно. Каждый раз, придя к фонтану и не встретив другого, человек сразу разворачивается и идёт обратно.
Так продолжается, пока они не встретятся у фонтана.

Нужно определить момент первой встречи у фонтана или вывести -1, если этого никогда не произойдёт.

Идея в двух шагах

Когда каждый из них бывает у фонтана?
- Маша: в моменты m, 3m, 5m, ... — нечётные кратные m.
- Паша: в моменты p, 3p, 5p, ... — нечётные кратные p.
Когда они встречаются?
Нужно найти первый момент времени, который встречается в обеих последовательностях:

Темы:
НОД/НОК, алгоритм Евклида, формулы, математика,
ОлПрактика lvl 2–3, Алгоритмы lvl 1, конструктив.

Код на 30 баллов:

m, p = int(input()), int(input())
if m < p: 
    p, m = m, p # swap(m, p) - поменяли местами m и p, чтобы было m >= p
t = m
# пока не перейдем через порог и пока t // n четное (надо наоборот)
while t <= 2 * m * t and (t // n) % 2 == 0:
    t += 2 * m # двигаемся по большему числу
if (t // n) % 2 == 1:
    print(t)
else:
    print(-1)

В целом это решение у многих набирало до 60 баллов на C++.

Те, кто доходил до этой стадии, замечали, что ответ либо НОК, либо не существует.

Опять же, на олимпиадах по программированию вредно пытаться доказывать факт вручную — это съедает и силы, и время. Логичнее сразу проверить гипотезу с НОК, а затем просто погонять решение на разных тестах: ответ получится либо -1, либо сам НОК.

К сожалению, на ВСОШ, похоже, были плохо настроены тесты, и некоторые наши ученики получили 100 баллов за неверное решение.
Идея была такая:

если НОК нечётный — вывести его;
если НОК чётный — вывести -1.

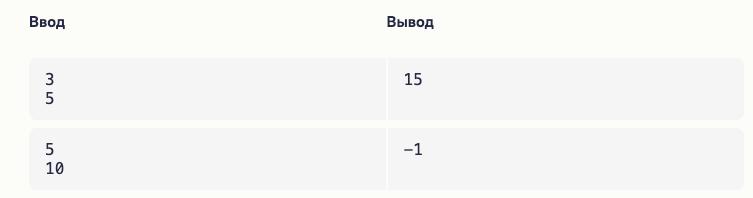
Однако это не работает, например, для теста:
$m = 6$, $p = 10$.

Тогда встреча произойдёт так:

6 → 18 → 30

10 → 30

Итог: кому-то повезло сдать неверный код

def nod(a, b): # Это алгоритм Евклида
    while a != 0 and b != 0:
      a, b = b, a % b
    return a + b

def max_digit2(x):
# степень двойки, на которую делится x, то есть 2**c
    c = 0
    while x % 2 == 0:
      x //= 2
      c += 1
    return c

m, p = int(input()), int(input())

if max_digit2(m) != max_digit2(p):
    print(-1)
else:
    # первая встреча у фонтана — NOK(m, p)
    nok = m * p // nod(m, p) 
    # пользуемся фактом, что m * p = NOD(m, p) * NOK(m, p)
    print(nok)

Задача D. Раскраска стены

Короткое условие:

Есть стена из n рядов по m клеток. Кирпич — это горизонтальное домино размером 1 х 2.
Ряды сдвинуты на одну клетку относительно соседних. На концах ряда могут быть «половинки» кирпича (1 клетка из двух).
В самом нижнем ряду слева стоит целый кирпич.

Нужно раскрасить кирпичи в минимальное количество цветов так, чтобы любые два соседних кирпича
(имеющие общую вертикальную грань или любой общий отрезок по горизонтали)
имели разные цвета.

В ответ нужно вывести n строк по m цифр (1–9), где клетки одного кирпича обозначаются одной и той же цифрой.

Идея для решения:

Если n = 1, то ответ 2 – идет просто чередование. В ином любом случае достаточно трех цветов.

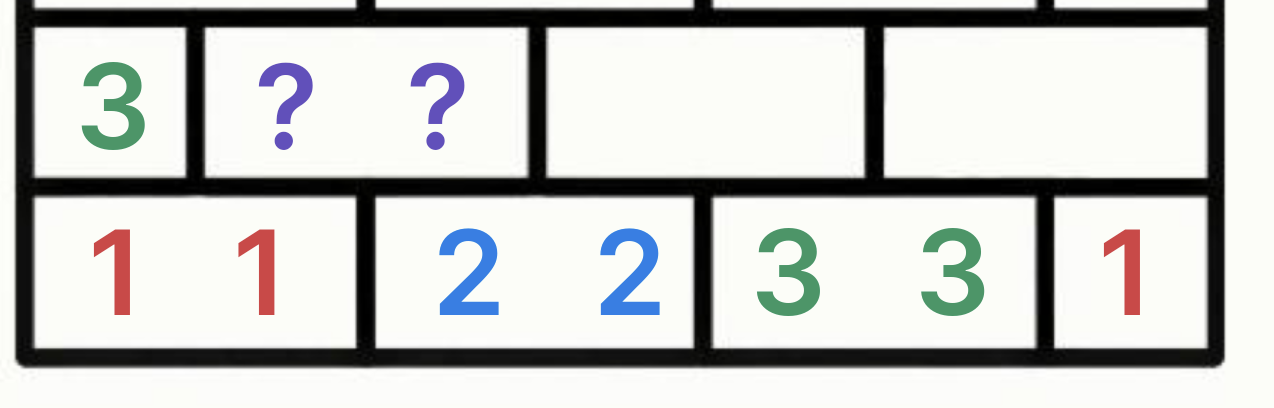
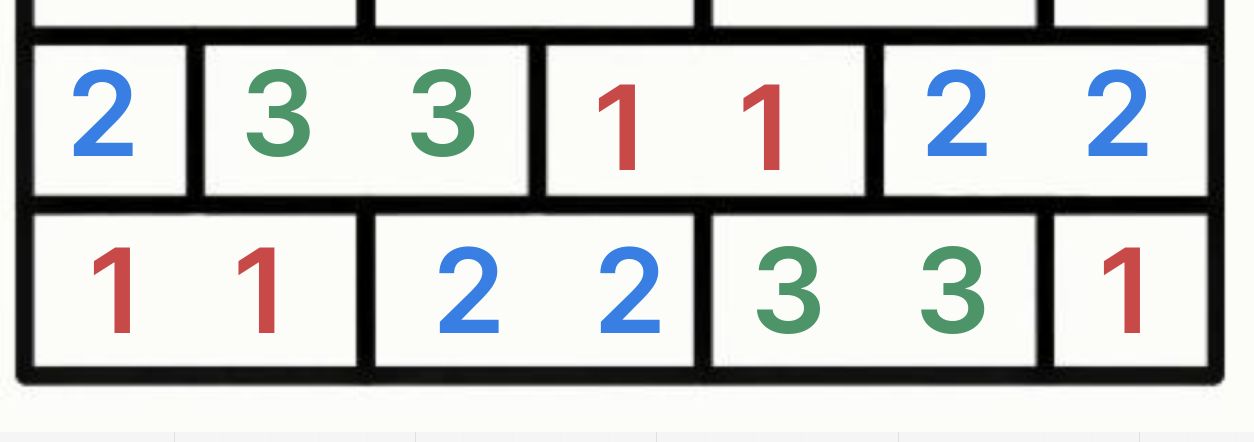
Легко заметить, что первые ряд мы можем закрасить как 1 1, далее 2 2, далее 3 3, далее снова 1 1, 2 2, 3 3, 1 1 и так далее пока не выведем m цифр.

Это будет нижний наш слой.

Слой над ним будет строить за счет жадность. Заметим, что мы не можем начинать с единицы этот ряд. Иначе будет пересечение. Соответсвенно у нас есть два варианта, начать либо с 2, либо 3.

Если мы начнем следующую строку с 3, то мы получаем ситуацию. Когда далее ни 1, ни 2 поставить нельзя. Соответственно требуется ввести новый цвет — 4.

Это плохо… Попробуем поставить 2. И далее выходит все с тремя цветами.

То есть, вторая строка будет выглядеть 2, и далее 3 3, затем 1 1, далее 2 2 и далее с чередованием. Теперь мы будем повторять первую строчку, затем вторую, затем первая строка,затем вторая

Темы: конструктив, строки, жадность
Курсы: Python Pro, ОлПрактика lvl 1–2

n, m = int(input()), int(input())
# Шаг 1 генерируем нужную строку 1 
# Можно сделать жадно 
# сделали строку с запасом на 24 символов, чтобы выводить часть строки
first = ('112233' + '112233') * 2 
second = ('233112' + '233112') * 2

# идем с последней строки (так как нижняя это по сути нулевая)
for i in range(n - 1, -1, -1):
    for j in range(0, m):
      if i % 2 == 0: # помним, что последняя строка - это по сути нулевая
                     # т.е. четные индексы у нас такого же типа как первая
        print(first[j], end = '')
      else:
        print(second[j], end = '')
    print()

Задача E. Проблема логистики

Короткое условие:

Темы: жадность, сортировки, multiset
Курсы: C++ Pro, Алгоритмы уровень 3, ОлПрактика уровень 4–5

Идея и ключевое наблюдение:

Если k супер большое, то очевидно можно действовать жадным алгоритмом:

Проблемы возникают когда наибольшему W нельзя сопоставить наибольший P.

Тут разберем решение на 60 баллов:

Действовать будем все также жадно (отсортировав оба массива по не возрастанию)

Идея решения логична, и первым шагом на олимпиаде было просто её проверить. К сожалению, многие ребята пытались сразу доказывать её в голове, что занимало время и силы.

Главное оружие программиста — хорошая интуиция и способность опираться на ассоциации. В этой задаче доказать идею несложно, и это можно сделать самостоятельно.

Некоторые ребята пытались улучшить решение и за счёт оптимизаций набирали до 75 баллов.

Код O(n * k) — на 60-75 баллов:

def calc(n, k, W, P):
    W.sort(reverse=True) # тяжёлые контейнеры первыми
    P.sort(reverse=True) # дорогие машины первыми

    ans = 0

    for w in W:
        j_ans = -1
        for j in range(len(P)):
            if w * P[j] <= k and j_ans == -1:
                j_ans = j

        if j_ans == -1:
           return -1 # не нашли ни одной подходящей машины
        ans += w * P[j_ans]
        P.pop(j_ans) # удаляем занятую машину

    return ans

n, k = map(int, input().split())
W = list(map(int, input().split()))
P = list(map(int, input().split()))

print(calc(n, k, W, P))

Решение задачи Е на 100 баллов:

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios::sync_with_stdio(false); // быстрый ввод вывод
    cin.tie(nullptr);

    int n;
    long long k;
    cin >> n >> k;

    vector<long long> W(n), P(n);
    for (int i = 0; i < n; ++i) cin >> W[i];
    for (int j = 0; j < n; ++j) cin >> P[j];

    sort(W.rbegin(), W.rend());

    multiset<long long> ms(P.begin(), P.end()); // положили весь P внутрь multiset
    long long total = 0;

    for (long long w : W) {
        long long max_price = k / w;

        // Найти наибольшую цену <= max_price:
        // upper_bound(max_price) -> первый элемент > max_price.
        auto it = ms.upper_bound(max_price); // Немного плюсовой магии
        if (it == ms.begin()) { // все цены > max_price
           cout << -1 << '\n';
           return 0;
        }
        --it; // теперь *it <= max_price — максимально возможная
        // Когда вычитаем из итератора один - мы переходим на первую цену, что меньше

        total += w * (*it);
        ms.erase(it);
    }

    cout << total << '\n';
    return 0;
}

Пробное занятие
с репетитором по математике и программированию

Запишитесь сейчас бесплатно

Записаться

Понравилась статья?

Подпишись на Телеграм школы, чтобы не пропустить новые статьи и новости

Telegram канал