Разбор муниципального этапа ВсОШ 2025-2026 по информатике (программированию) от ЮАЙТИ
17.12.2025
Задача 1. Большой квадрат
Краткий пересказ условия
Даны два прямоугольника размеров $a × b$ и $c × d$
• Каждый прямоугольник можно повернуть (поменять местами стороны).
• Затем прямоугольники можно склеить, приложив сторону к стороне (длины сторон могут различаться — склеивается только общая часть).
• Из получившейся фигуры нужно вырезать квадрат, причём стороны квадрата параллельны сторонам прямоугольников.
Нужно найти максимально возможную сторону такого квадрата.
Темы
• формулы, математика
• перебор
• геометрические конструкции
Уровень относительно курсов: Python Start + ОлПрактика lvl 1-2
Шаг 0. Договоримся, что высота — большая сторона
Даны прямоугольники a×b и c×d. Прямоугольник можно повернуть, поэтому мы можем сделать так:
• если a < b, поменяем местами ⇒ теперь a ≥ b
• если c < d, поменяем местами ⇒ теперь c ≥ d
После этого удобно думать так:
• 1‑й прямоугольник: высота = a, ширина = b (и b — меньшая сторона)
• 2‑й прямоугольник: высота = c, ширина = d (и d — меньшая сторона)
Почему после этого выгодно склеивать именно по высотам
Квадрат может быть большого размера только если ему хватает места по высоте и по ширине.
Если мы хотим квадрат, который использует оба прямоугольника, то он обязательно должен лежать в области, где прямоугольники перекрываются по одной из сторон (по высоте или по ширине — зависит от того, как мы их склеим).
Важное наблюдение
Если мы склеим так, что общая перекрывающаяся сторона будет маленькой (например, min(b, d)- одной из широт прямоугольников), то квадрат, который пересекает шов, будет ограничен этой маленькой величиной:
$side \leq min(b, d)$
А это не больше, чем $b$ или $d$.
То есть в таком случае выгоднее (или не хуже) просто вырезать квадрат целиком из одного прямоугольника.
✅ Значит единственный вариант, который может дать квадрат больше, чем $b$ и $d$ — это склеить прямоугольники так, чтобы они перекрывались по большим сторонам: по высотам $a$ и $c$.
Ключевая идея
У квадрата всего три типа расположения в получившейся фигуре:
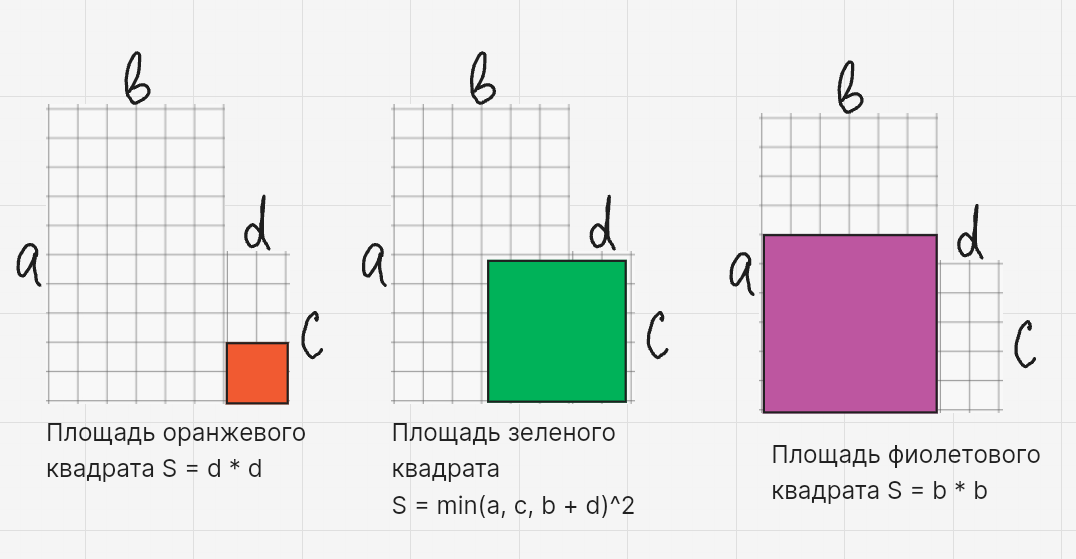
1. Квадрат целиком внутри первого прямоугольника (оранжевый квадрат на рисунке)
Тогда максимум — это просто $min(ширина1, высота1)$
2. Квадрат целиком внутри второго прямоугольника (фиолетовый квадрат на рисунке)
Максимум — $min(ширина2, высота2)$
3. Квадрат пересекает шов склейки (то есть часть квадрата в одном прямоугольнике, часть — в другом).
(зеленый квадрат на рисунке)
Это единственный случай, когда квадрат может получиться больше, чем любой из прямоугольников по отдельности.
Дальше важно заметить: если квадрат пересекает шов, то на каждой высоте (на каждом $y$ внутри квадрата) он пересекает шов тоже. Значит, на всех этих $y$ должны существовать оба прямоугольника одновременно. То есть квадрат обязан целиком уместиться в общей (перекрывающейся по высоте/ширине) полосе двух прямоугольников.
Почему это точно правильно
• Любой квадрат либо целиком в одном прямоугольнике → это b или d.
• Либо он использует оба → тогда он обязательно ограничен:
– общей шириной (не больше b+d)
– общей высотой перекрытия (не больше min(a,c) если мы склеиваем по высотам)
• Любые другие способы склейки дают перекрытие не больше $min(b,d)$ и не могут дать квадрат больше, чем уже дают варианты b и d.
Сложность
• Временная: O(1) (всего 4 ориентации и несколько min/max)
• Память: O(1)
Код на Python
a, b, c, d = int(input()), int(input()), int(input()), int(input())
if a < b: # делаем так, чтобы a была больше равна b (a ≥ b)
a, b = b, a
if c < d: # аналогично c ≥ d
c, d = d, c
val = min(a, c, b + d)
print(max(b, d, val))Задача 2. План эвакуации
Пересказ условия
Есть этаж здания в виде прямоугольной сетки n × m комнат. Из каждой комнаты можно пройти в соседнюю (вверх, вниз, влево, вправо), если сосед существует.
В двух комнатах находятся лестницы. Нужно для каждой комнаты указать одно направление движения в соседнюю комнату так, чтобы:
• если из любой комнаты идти строго по стрелкам, то мы точно дойдём до одной из лестниц;
• путь получится минимальной длины (то есть равен кратчайшему расстоянию до ближайшей лестницы).
В клетках с лестницами надо вывести символ S, в остальных — стрелку $<, >, \^, v$
Можно вывести любой подходящий план.
Темы
• Формулы, математика
• Вложенные циклы, строки, символы
• Геометрические конструкции
Уровень относительно курсов: Python Pro + ОлПрактика lvl 1-2
Главное наблюдение (очень важное)
В этой задаче нет стен и препятствий: решётка полностью проходимая.
Значит, кратчайшее расстояние от комнаты (i, j) до лестницы (r, c) — это просто манхэттенское расстояние:
$dist = |i — r| + |j — c|$
Почему? Потому что каждый шаг меняет строку или столбец на 1, и чтобы совместить и строку, и столбец, нужно ровно столько шагов, сколько суммарная разница.
Как построить стрелки
Пусть лестницы стоят в клетках A(r1, c1) и B(r2, c2).
Для каждой комнаты (i, j):
• Считаем расстояния до обеих лестниц:
$d1 = |i-r1| + |j-c1|$
$d2 = |i-r2| + |j-c2|$
• Выбираем ближайшую лестницу:
если $d1 <= d2$, считаем, что идём к первой, иначе — ко второй.
(Если расстояния равны — можно выбрать любую, мы выберем первую.)
• Ставим стрелку так, чтобы сделать один шаг ближе к выбранной лестнице:
— если мы выше нужной лестницы $i < r$ — нужно двигаться вниз: v
— если ниже $i > r$ — вверх: ^
— иначе (строки равны), если $j < c$ — вправо: >
— иначе — влево: <
Визуализацию можно посмотреть на двух гифках, в них любая из точек выбирает ближайшую лестницу, далее либо поднимается, либо спускается до нужной высоты, затем идет уже полностью либо влево, либо вправо.

Почему это правильно
1) Мы обязательно дойдём до лестницы
Мы всегда делаем шаг, который уменьшает расстояние $|i-r| + |j-c|$ на 1.
Расстояние — число неотрицательное. Значит, оно будет уменьшаться, уменьшаться… и в какой-то момент станет 0.
А расстояние 0 бывает только в самой клетке лестницы.
То есть зацикливаться невозможно: расстояние строго падает.
2) Путь будет кратчайшим
Если из клетки расстояние до выбранной лестницы равно $d$, то мы уменьшаем его на 1 каждый шаг и придём ровно за $d$ шагов.
А меньше, чем $d$, пройти нельзя (это и есть кратчайшее расстояние).
Значит, наш путь — минимальный.
Алгоритм
• Считываем $n, m, r1, c1, r2, c2$
Для каждой клетки:
• если это лестница → печатаем $S$
• иначе → считаем $d1$, $d2$, выбираем лестницу и печатаем стрелку в её сторону
• выводим сетку.
Сложность
• Время: $O(n·m)$ — просто пробегаем все клетки.
• Память: $O(1)$ (или $O(n·m)$, если хранить сетку — но можно печатать сразу).
Код на Python
n, m = int(input()), int(input())
r1, c1, r2, c2 = int(input()), int(input()), int(input()), int(input())
for i in range(1, n + 1):
for j in range(1, m + 1):
# из i j мы хотим попасть либо r1 c1 либо r2 c2
# считаем расстояния до лестниц
d1 = abs(i - r1) + abs(j - c1)
d2 = abs(i - r2) + abs(j - c2)
if d1 == 0 or d2 == 0:
print('S', end = '')
continue
r, c = r1, c1 # то куда побежим
if d1 > d2:
r, c = r2, c2
# Делаем шаг, который уменьшает расстояние до (r, c)
if i > r:
print('^', end = '')
elif i < r:
print('v', end = '')
elif j < c:
print('>', end = '')
else:
print('<', end = '')
print()
Задача 3. Аркадий Аркадьевич делает грядки
Краткий пересказ условия
У Аркадия Аркадьевича есть $n$ досок, длина $i‑й — l[i]$
Он хочет выбрать 4 доски и сложить из них прямоугольную грядку.
• В идеале нужны две пары одинаковых сторон: тогда прямоугольник собирается без проблем.
• Если в паре доски разной длины, можно поставить пластиковый уголок размера $r$ в одном углу: он позволяет “удлинить” две соседние стороны на величину не больше $r$.
Если противоположными сторонами будут доски длины $a и b$, а другими противоположными — $c и d$, то минимально нужный уголок:
$r = max(|a — b|, |c — d|)$
Нужно найти минимально возможный $r$ и вывести любые подходящие 4 длины $a b c d$
Темы
• Жадность, сортировки
• Эффективный линейный поиск
• Реализация
Уровень относительно курсов: Алгоритмы lvl 1 / Алгоритмы lvl 3 + ОлПрактика lvl 2-3
Тема эффективный линейный поиск встречается и на более ранних этапах, чем в lvl 3. Но та идея, что нужна здесь, она считается сложной в плане реализации (если мы говорим про решение на 100).
С ней связаны десятки популярных задач на темы динамики, префиксных подсчетов и тд. И порой очень сильные программисты не знают как решить такую задачу, если ее немного усложнить.
(Проверено в прошлом году на призерах ВСОШ: придумать в итоге придумали, но заняло очень много времени)
Поэтому задача не очень сложная и сложная одновременно.
Разбор простой — наслаждайтесь.
Главная идея
Чтобы уголок был маленьким, нужно, чтобы в каждой паре доски были как можно ближе по длине друг к другу.
И вот ключевое наблюдение:
Наблюдение 1
Если мы отсортировали длины по возрастанию, то в хорошем ответе пары будут состоять из соседних элементов.
• Представьте, что в паре стоят доски $x и y$, и между ними есть доска $z (x ≤ z ≤ y)$
• Тогда разница |x-y| не меньше, чем |x-z|
• Значит, выгоднее (или хотя бы не хуже) взять $x и z$, чем $x и y$.
И да, мы не математики, нам так говорить можно
То есть перепрыгивать через доски внутри пары смысла нет: всегда можно заменить на более близкую.
Во что превращается задача
Теперь мы выбираем две непересекающиеся соседние пары:
• первая: (a$[i]$, a$[i+1]$)
• вторая: (a$[j]$, a$[j+1]$)
• пары не должны пересекаться ⇒ j ≥ i+2
А значение уголка: r=max(a$[i+1]$−a$[i]$, a$[j+1]$−a$[j]$). Нужно минимизировать это r.
Решение на 100 баллов (n до 1e5)
Как найти две пары быстро
Перебрать все $i, j$ в лоб — это $O(n^2)$ (для 1e5 не подойдёт).
Но уже это решение набирало не менее 65 баллов.
Идея за линию O(n).
• Пусть мы зафиксировали пару подряд элементов $(i, i+1)$
Для нее надо найти пару элементов левее, у которых разница между собой минимальна (идеально ноль)
• Заметим, нет необходимости искать пару правее, ведь когда мы зафиксируем пару правее — то наша пара $(i, i+1)$ является теперь слева
• То есть если мы пойдем перебирать пары $(i, i+1)$ слева направо, то нам требуется поддерживать пару чисел у которых минимальная разница
• А зная ее, можем посчитать ответ для пары элементов $(i, i+1)$ , которые хотим взять
Почему это правильно (коротко)
Для фиксированного $j$ значение $max(D[i], D[j])$ тем меньше, чем меньше $D[i]$
Значит среди всех допустимых $i$ лучше всего брать тот, где $D[i]$ минимально — а это и есть $prefMin[j-2]$
Сложность
• сортировка: $O(n log n)$
• один проход по массиву: $O(n)$
• память: $O(n)$
Как найти ответ за один проход — O(n)
Идём слева направо и считаем пары “справа”.
Пусть мы сейчас рассматриваем правую пару $(a[i], a[i+1])$
(где i идёт от 2 до n-2)
Тогда левая пара обязана лежать левее, то есть начинаться не позже $i-2$
Чтобы $max(левая_разница, правая_разница)$ было минимальным, для фиксированной правой пары выгоднее всего взять левую пару с минимальной разницей среди всех допустимых слева.
Поэтому мы просто поддерживаем:
$best\_left\_diff$ — минимальная разница среди уже пройденных соседних пар слева
$best\_left\_pos$ — где эта пара начинается (индекс)
На каждом $i$
• считаем $right\_diff = a[i+1]-a[i]$
• кандидат: $cur = max(best\_left\_diff, right\_diff)$
• обновляем лучший ответ
• обновляем $best\_left\_diff$ добавляя новую левую пару $(a[i-1], a[i])$
Почему пары не пересекаются
Когда мы на шаге i берём правую пару (i, i+1), то левую мы храним только из пар, которые заканчиваются максимум в i (то есть начинаются максимум в i-1), а реально допустимые — до i-2.
В таком проходе это соблюдается автоматически: лучшая левая считается до использования текущей правой.
Сложность
• сортировка: $O(n log n)$
• один проход: $O(n)$
• память: $O(n)$ на сами длины, без массива разниц
Код на Python
n = int(input())
a = [0] * n
for i in range(n):
a[i] = int(input())
a.sort()
# лучшая (самая маленькая) разница среди левых соседних пар
best_left_diff = a[1] - a[0]
best_left_pos = 0 # пара (a[0], a[1])
best_r = 10**18
ans_i = 0
ans_j = 2 # правая пара начнётся минимум с 2
for i in range(2, n - 1): # правая пара: (a[i], a[i+1])
right_diff = a[i + 1] - a[i]
cur = best_left_diff
if right_diff > cur:
cur = right_diff # cur = max(best_left_diff, right_diff)
if cur < best_r:
best_r = cur
ans_i = best_left_pos
ans_j = i
# обновляем лучшую левую пару, добавляя пару (a[i-1], a[i])
left_diff = a[i] - a[i - 1]
if left_diff < best_left_diff:
best_left_diff = left_diff
best_left_pos = i - 1
print(best_r)
print(a[ans_i], a[ans_i + 1], a[ans_j], a[ans_j + 1])Решения на частичные баллы
Ниже варианты, которые проще или медленнее, но подходят под ограничения подзадач.
✅ 20 баллов: $n ≤ 30$ (полный перебор 4 досок)
Идея:
• переберём первую пару $(x, y)$ и вторую $(u, v)$
• проверим, хватает ли досок по количеству
• $r = max(y-x, v-u)$ (если считаем x≤y, u≤v)
Код на Python
n = int(input())
a = [0] * n
for i in range(n):
a[i] = int(input())
best_r = 10**18
best_ans = []
for i in range(0, n):
for j in range(0, n):
for k in range(0, n):
for t in range(0, n):
# проверяем, что все индексы разные
if i == j or i == k or i == t or j == k or j == t or k == t:
continue # если не разные - то пропускаем
if a[i] <= a[j] <= a[k] <= a[t]:
d1 = abs(a[j] - a[i])
d2 = abs(a[t] - a[k])
if max(d1, d2) < best_r:
best_r = max(d1, d2)
best_ans = (a[i], a[j], a[k], a[t])
print(best_r)
print(*best_ans)
Это же решение на С++ набирало 45 баллов. Так как $100^4 = 100.000.000$, а С++ успеваем выполнить до 250-400 млн операций / секунда.
✅ 45/65 баллов: $n ≤ 100$ или $n ≤ 500$ (сортировка + перебор двух соседних пар за O(n²))
Уже используем главное наблюдение пары — соседи, но ещё без оптимизаций.
• сортируем
• перебираем $i и j$ (где j ≥ i+2, чтобы пары не пересекались)
Для $n ≤ 500$ это нормально (~125 тысяч проверок).
Код на Python
n = int(input())
a = [0] * n
for i in range(n):
a[i] = int(input())
a.sort()
best_r = 10**18
best_i = 0
best_j = 2
for i in range(0, n - 2):
for j in range(i + 2, n - 1):
d1 = a[i + 1] - a[i]
d2 = a[j + 1] - a[j]
r = max(d1, d2)
if r < best_r:
best_r = r
best_i = i
best_j = j
print(best_r)
print(a[best_i], a[best_i+1], a[best_j], a[best_j+1])
Задача 4. Гравитационная сортировка
Пересказ условия
Есть $n$ стержней и $n$ чисел $a1, a2, …, an$ (каждое $0 ≤ ai ≤ n$).
Мы раскладываем бусинки так:
• в 1‑м ряду (самом нижнем) кладём бусинки на самые левые $a1$ стержней,
• во 2‑м ряду — на левые $a2$
• …
• в $n$‑м ряду — на левые $an$
Потом все бусинки одновременно начинают падать вниз по стержням.
За 1 секунду бусинка опускается на 1 ряд вниз, если:
• снизу пусто или
• снизу стоит бусинка, которая тоже в эту секунду опускается.
Нужно для каждого стержня вывести, через сколько секунд на этом стержне все бусинки перестанут двигаться.
Вывод: $n$ чисел, каждое на новой строке (как в примере).
Темы
• Сортировка подсчетом
• Словарь
• Линейные алгоритмы
Уровень относительно курсов: Алгоритмы lvl 1 / Алгоритмы lvl 3 + ОлПрактика lvl 3-5
Для понимания происходящего
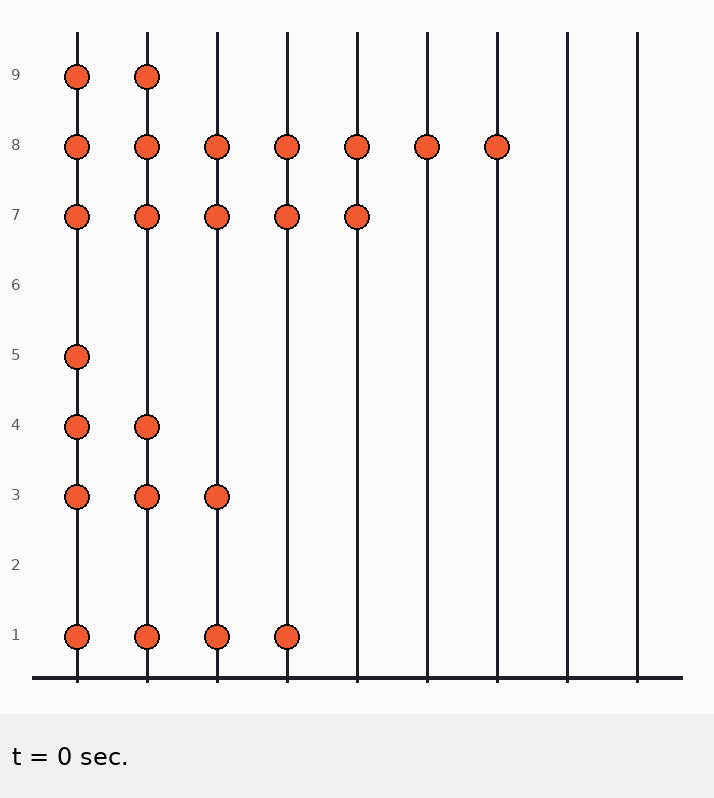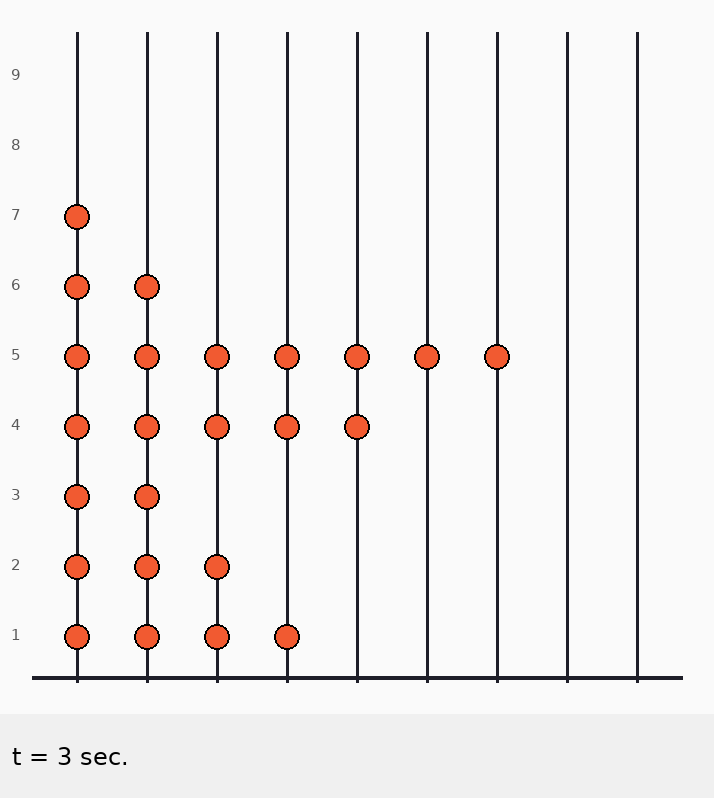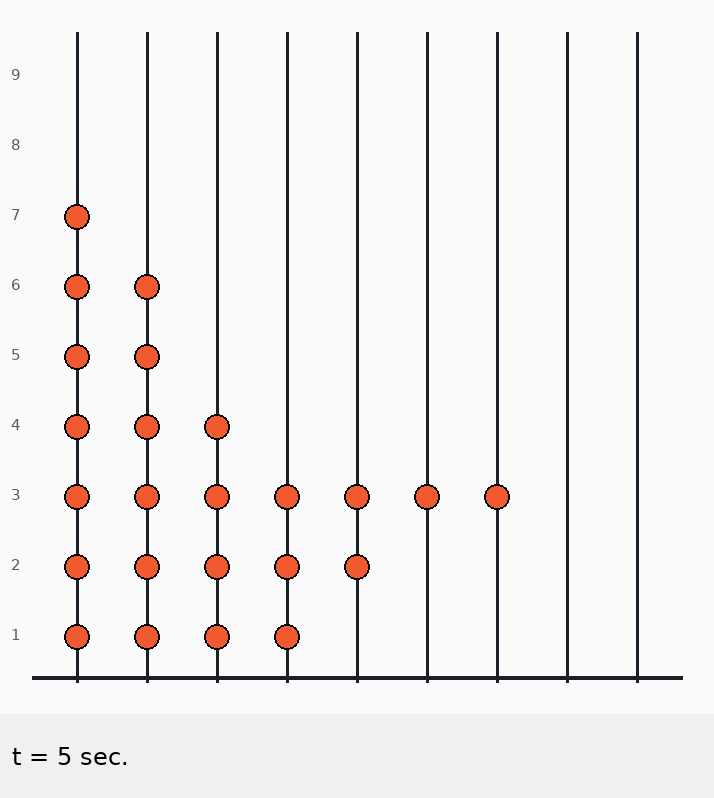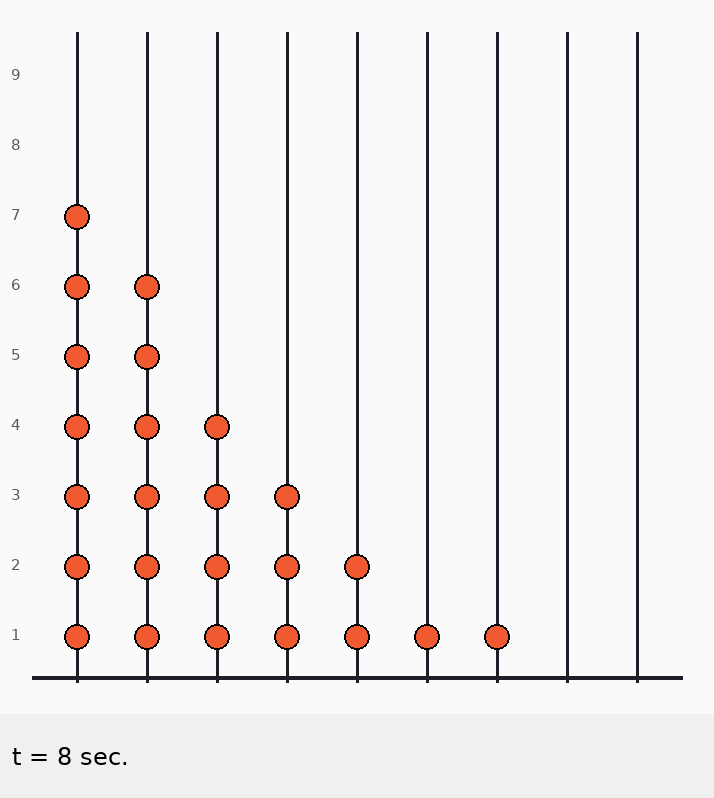
Главная идея: стержни независимы
Бусинки никогда не двигаются влево/вправо, только вниз.
Значит, можно рассматривать каждый стержень отдельно.
1) Что происходит на одном стержне (самое главное)
Возьмём один стержень j.
Где на нём стоят бусинки в начале?
В ряду i бусинка есть на стержне j тогда и только тогда, когда: $a_i \ge j$
Потому что в ряду i мы кладём бусинки на стержни 1..a_i.
2) Что будет после падения
На одном стержне бусинки не могут разойтись в стороны, они только падают вниз.
Значит в конце они обязательно окажутся снизу без дырок:
Если на стержне всего k бусинок, то финально они займут ряды:
$1,2,3,\dots,k$
(где ряд 1 — самый нижний)
3) Сколько секунд будет двигаться стержень j ?
Пусть на стержне j самая верхняя бусинка в начале стояла в ряду p (то есть это максимальный номер ряда, где a_i ≥ j).
• в конце верхняя бусинка будет стоять на уровне k
• значит она опустится на: $p — k$
Почему это и есть время остановки?
• бусинки падают максимум на 1 ряд за секунду,
• верхняя бусинка падает дольше всех (ей дальше всего до кучки снизу),
• значит стержень перестанет двигаться ровно через p-k секунд.
✅ Ответ для стержня j:
$T_j = p_j — k_j$
где
$k_j$ = сколько бусинок на стержне (сколько i таких, что $a_i ≥ j$)
$p_j$ = самый верхний ряд с бусинкой (max i таких, что $a_i ≥ j$)
4) Как найти $k_j$ и $p_j$ для всех стержней
Медленно (понятно, но O(n²))
Для каждого j пробежаться по всем i:
• если $a_i ≥ j$, то увеличиваем k
• и запоминаем p = i (последний такой ряд)
Это работает, но медленно при $n ≤ 20000$.
5) И вот тут появляется cnt: он просто ускоряет подсчёт
Мы хотим быстро знать для каждого j:
• сколько значений $a_i$ не меньше j
• и какой у них самый большой индекс i
Вместо того чтобы каждый раз заново сканировать a, мы заранее делаем табличку частот.
Что такое cnt$[x]$
cnt$[x]$ = сколько раз встречается число x в массиве a.
(подсчет значений через словарь или через сортировку подсчетом)
Например, если a = $[2,4,1,5,3]$, то:
• cnt$[1]$=1, cnt$[2]$=1, …, cnt$[5]$=1
Что такое last$[x]$
last$[x]$ = в каком самом позднем ряду стоит значение x.
Например, в a = $[2,4,1,5,3]$:
• last$[2]$=1 (2 стоит в ряду 1)
• last$[5]$=4 (5 стоит в ряду 4)
• и т.д.
Почему мы идём по j справа налево: от n к 1
Посмотри на множества:
• для j = 5 нам нужны все $a_i ≥ 5$
• для j = 4 нам нужны все $a_i ≥ 4$ — это те же, плюс ещё $a_i = 4$
• для j = 3 — те же, плюс ещё $a_i = 3$
• …
То есть когда мы уменьшаем j, множество $a_i ≥ j$ расширяется постепенно.
Поэтому можно поддерживать две переменные:
• count = сколько уже добавили чисел (это и будет k_j)
• maxpos = максимальный индекс среди уже добавленных (это и будет p_j)
И обновления очень простые: при переходе к j добавляются все элементы, где a_i == j; их количество = cnt$[j]$, значит:
count += cnt$[j]$
А самый поздний индекс среди новых добавленных = last$[j]$, значит:
maxpos = \max(maxpos,\ last $[j]$)
И после этого:
$T_j = maxpos — count$
Небольшой пример, чтобы увидеть связь
n = 5
a = [2, 4, 1, 5, 3] (ряды снизу вверх)Тогда:
• cnt$[5]$=1, last$[5]$=4
• cnt$[4]$=1, last$[4]$=2
• cnt$[3]$=1, last$[3]$=5
• cnt$[2]$=1, last$[2]$=1
• cnt$[1]$=1, last$[1]$=3
Идём j = 5 → 1:
j = 5
• count += cnt$[5] $= 1 → count=1 (на стержне 5 ровно 1 бусинка)
• maxpos = max(0, last$[5]$=4) → maxpos=4 (самая верхняя бусинка в ряду 4)
• T5 = 4 — 1 = 3
j = 4
• count += cnt$[4]$=1 → count=2 (на стержне 4 бусинок 2)
• maxpos = max(4, last$[4]$=2)=4
• T4 = 4 — 2 = 2
j = 3
• count += 1 → 3
• maxpos = max(4, last$[3]$=5)=5
• T3 = 5 — 3 = 2
j = 2
• count=4, maxpos=5
• T2 = 5 — 4 = 1
j = 1
• count=5, maxpos=5
• T1 = 5 — 5 = 0
Вот и ответы.
7) Связь cnt с ответом
cnt нужен, чтобы быстро (без сканирования массива) узнать, сколько рядов добавляется при переходе к очередному j, то есть быстро считать k_j, а через last — быстро считать p_j.
А ответ всегда $T_j = p_j — k_j$.
Еще один пример, если вам необходим, то станет в РАЗЫ понятнее. Если уже все ок, просто двигайтесь далее.
n = 6
a = $[3, 2, 1, 4, 3, 2]$
(ряд 1 — снизу, ряд 6 — сверху)
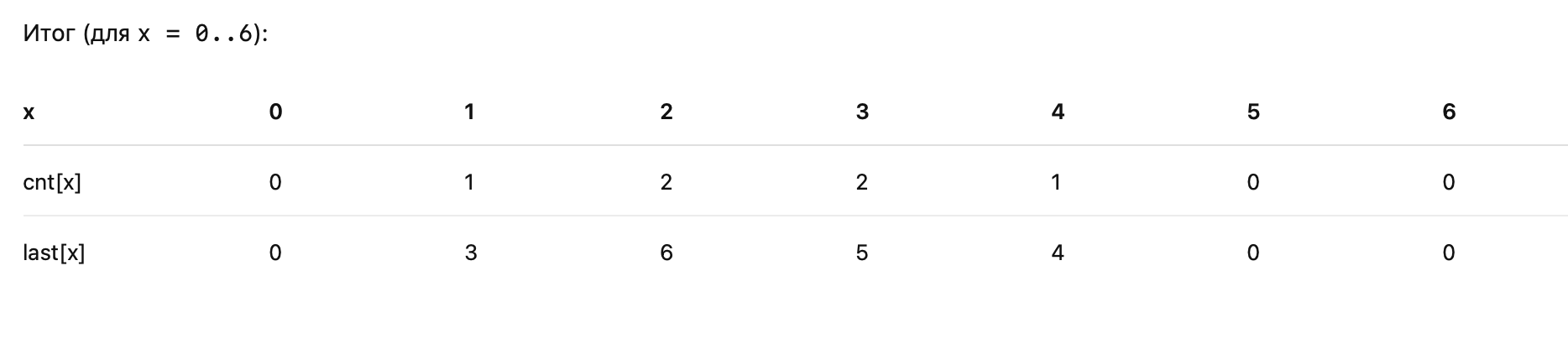
1) Считаем cnt и last
Что означает:
• cnt$[x]$ — сколько раз встречается число x в массиве a
• last$[x]$ — самый большой номер ряда i, где ai = x (самое верхнее появление)
Проходим снизу вверх:
2) Идём по стержням справа налево: j = 6 … 1
Напоминание:
• count = сколько ai ≥ j → это k_j (сколько бусинок на стержне j)
• maxpos = максимальный индекс i среди ai ≥ j → это p_j (самая верхняя бусинка)
Ответ:
$T_j = p_j — k_j = maxpos — count$
Старт: count = 0, maxpos = 0.
3) Ответы (стержни 1..6)
• T1 = 0
• T2 = 1
• T3 = 2
• T4 = 3
• T5 = 0
• T6 = 0
Сложность
Время: $O(n)$
Память: $O(n)$
Код на 100 баллов (Python 3, простой)
n = int(input())
a = list(map(int, input().split()))
cnt = [0] * (n + 1)
last = [0] * (n + 1) # last[x] = последний индекс, где ai = x (1..n)
# сортировка подсчетом - считаем сколько каждый элемент встречается раз и где последний
for i range(n):
cnt[a[i]] += 1
last[a[i]] = i
count = 0 # сколько ai >= j
maxpos = 0 # max индекс среди ai >= j
ans = [0] * n
for j in range(n, 0, -1):
count += cnt[j]
if last[j] > maxpos:
maxpos = last[j]
ans[j - 1] = maxpos - count # наше время
print(*ans, sep = '\n')Почему формула $T = maxpos — count$ работает
На стержне:
• $count$ бусинок → в конце они займут места $1..count$
• самая верхняя бусинка была в ряду $maxpos$ → в конце окажется в ряду $count$
• значит ей падать $maxpos — count$ секунд
А она падает дольше всех → это и есть ответ.
Решения на частичные баллы
В этой задаче в системе оценки указаны подзадачи:
✅ $n ≤ 10$ — 30 баллов
✅ $n ≤ 2000$ — 60 баллов
✅ $n ≤ 100000$ — 100 баллов (полное решение выше)
Ниже варианты специально под них.
1) 30 баллов (n ≤ 10): честная симуляция падения
Можно просто для каждого стержня построить столбик из 0/1 и симулировать секунды: за секунду пузырьком опускаем бусинки на 1 вниз, если снизу пусто. И считаем, сколько секунд нужно, пока столбик не перестанет меняться.
Код на Python
n = int(input())
a = list(map(int, input().split()))
res = []
for j in range(1, n + 1):
# col[i] = 1, если на стержне j есть бусинка в ряду (i+1)
col = [0] * n
for i in range(n):
if a[i] >= j:
col[i] = 1
t = 0
go = True
while go:
moved = False
# один "тик": если снизу пусто и сверху бусинка — меняем местами
for i in range(n - 1):
if col[i] == 0 and col[i + 1] == 1:
col[i] = 1
col[i + 1] = 0
moved = True
if not moved:
go = False
t += 1
res.append(t)
print(*res, sep = '\n')Почему это подходит для $n ≤ 10$:
Стержней 10, высота 10, секунд максимум тоже ≤ 10 → всё очень маленькое.
2) 60 баллов (n ≤ 2000): посчитать $count$ и $maxpos$ в лоб за O(n²)
Для каждого стержня $j$ просто пробегаем все ряды: если ai ≥ j, то count++ и maxpos = i
Потом печатаем $maxpos — count$
n стержней × n рядов = O(n²) для 2000 это примерно 4 млн проверок (нормально).
Код на Python
n = int(input())
a = list(map(int, input().split()))
for j in range(1, n + 1):
count = 0
maxpos = 0
for i in range(1, n + 1):
if a[i - 1] >= j:
count += 1
maxpos = i
print(maxpos - count)Задача 5. Шифр mint
Пересказ условия
Есть 18 букв: A, B, …, R. Петя шифрует каждую букву уникальным числом из набора:
${1,2,3,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90}$
• одинаковые буквы → одинаковые числа
• разные буквы → разные числа
Шифр строки — это просто приписывание кодов подряд (конкатенация).
Нужно выбрать шифр так, чтобы получившееся число было минимально (число может быть очень длинным, сравниваем как строку цифр).
Темы
• Словари, множества
• Жадность
• Рекурсивный перебор
Уровень относительно курсов: Алгоритмы lvl 2 + ОлПрактика lvl 4-6
Шаг 1: сначала минимизируем длину
У нас нет ведущих нулей, поэтому любое число с меньшим количеством цифр всегда меньше любого числа с большим количеством цифр.
Значит цель такая:
1. сделать шифр самой короткой длины
2. среди них — самый маленький по лексикографическому порядку (как строки)
Шаг 2: Как длина зависит от выбора коротких букв
Пусть буква встречается cnt раз.
• если она короткая → даёт cnt * 1 цифр
• если длинная → даёт cnt * 2 цифр
То есть если буква длинная, она добавляет на cnt цифр больше, чем если бы была короткой. Чтобы итоговая длина была минимальной, короткие коды надо отдать буквам, которые встречаются чаще всего.
Если разных букв ≤ 9, тогда всем буквам можно дать короткие коды 1..9. Это очевидно оптимально по длине: длинные коды вообще не нужны.
Если разных букв > 9, коротких кодов всего 9, значит ровно 9 букв будут короткими, остальные длинными. Чтобы длина была минимальной, нужно выбрать 9 букв с максимальной суммой частот.
Обозначим:
$sumShort = \sum_{буква\ короткая} cnt[буква]$
Тогда длина шифра равна:
• базово $|s|$ цифр (как если бы все были короткими),
• плюс по 1 лишней цифре за каждое появление длинной буквы. Лишних цифр будет $|s|$ – sumShort.
Значит:
$len = |s| + (|s| — sumShort) = 2|s| – sumShort$
Минимизировать len — то же самое, что максимизировать sumShort.
Шаг 3: Почему всё равно нужен перебор
Иногда есть ничьи: разные наборы из 9 букв дают одинаковый sumShort, а значит одинаковую минимальную длину. Но сами числа могут получаться разными (из‑за того, какие буквы стали короткими и где они впервые встречаются).
Поэтому мы делаем так:
• Находим BEST_SUM — максимально возможное sumShort (это сумма 9 самых больших частот).
• Перебираем, какие 9 букв сделать короткими, но оставляем только те варианты, где sumShort == BEST_SUM.
• Для каждого такого варианта строим шифр и берём минимальный.
Шаг 4: Как строится минимальный шифр для фиксированного выбора коротких букв
Допустим, мы уже решили: какие буквы короткие, какие длинные.
Тогда минимальное число строится жадно по строке слева направо:
• если встретили новую короткую букву → даём ей самый маленький свободный код из 1..9 (сначала 1, потом 2, …)
• если встретили новую длинную букву → даём ей самый маленький свободный код из 10,20,… (сначала 10, потом 20, …)
Первое появление буквы — самое раннее место, где её код влияет на результат, если в этом месте поставить код больше, число сразу станет больше, и потом это уже “не исправить”. Поэтому encode() в решении — это просто один проход по строке.
Шаг 5: Рекурсивный перебор; взять букву в короткие / не взять.
Мы перебираем список разных букв letters.
Будем хранить массив used$[]$:
• used$[i]$ = 1 → letters$[i]$ короткая
• used$[i]$ = 0 → длинная
Функция перебора:
perebor(i, chosen_short, sum_short), где
• i — какую букву сейчас рассматриваем,
• chosen_short — сколько уже выбрали коротких,
• sum_short — сумма частот выбранных коротких букв.
База рекурсии
Когда chosen_short == 9, мы выбрали ровно 9 коротких букв.
• Если sum_short != BEST_SUM, этот вариант даёт длину хуже, его даже не проверяем.
• Если sum_short == BEST_SUM, строим шифр функцией encode() и обновляем лучший ответ.
Отсечение №1: не успеем набрать 9 коротких
Если осталось $k — i$ букв, то максимум коротких, что ещё можно набрать:
$chosen\_short + (k — i)$
Если это < 9 — дальше смысла нет, выходим.
Отсечение №2: даже в лучшем случае не догоним
BEST_SUM
Пусть нам ещё нужно добрать $need = 9 — chosen\_short$ коротких букв.
Среди оставшихся букв можно взять need самых частых (это идеальный случай).
Если
$sum\_short + maxPossible < BEST\_SUM$
то никакой выбор дальше не даст минимальную длину — выходим.
В коде maxPossible считается просто: берём частоты оставшихся букв, сортируем и суммируем need самых больших. Это нормально, потому что букв максимум 18.
Шаг 6: Правильность по длине
Мы рассматриваем только те наборы 9 коротких букв, для которых sumShort == BEST_SUM, а это ровно те, что дают минимальную длину см. формулу $len = 2|s| — sumShort$
Правильность по минимальному числу
Для каждого такого набора мы строим минимальный возможный шифр жадно (по первому появлению букв). Среди всех кандидатов берём минимальный по строковому сравнению — значит это минимальное число среди всех минимальной длины. Значит ответ оптимальный.
Букв максимум 18.
• ветвей у перебора максимум 2^18 ≈ 262000 (на практике меньше из‑за отсечений),
• их ожидаемо равно количеству способов выбрать 9 коротких букв из 18 без повторов = $C^9_{18} = 48620 $
• encode() — один проход по строке, то есть $O(|s|)$
• encode() вызывается только на хороших листьях (где выбрано 9 и sumShort == BEST_SUM).
Количество операций итоговое около 50 млн операций, на С++ заходит, на Python нет. Для олимпиадных ограничений это проходит.
Псевдокод
посчитать cnt каждой буквы
letters = список разных букв
если len(letters) <= 9:
вывести жадно (все короткие)
иначе:
BEST_SUM = сумма 9 максимальных freq
perebor(i, chosen, sum):
если chosen == 9:
если sum == BEST_SUM:
cand = encode(used)
best = min(best, cand)
return
если i == len(letters): return
если chosen + (len(letters)-i) < 9: return
need = 9 - chosen
if sum + max_possible_from_rest(i, need) < BEST_SUM: return
used[i]=1; perebor(i+1, chosen+1, sum+cnt[letters[i]])
used[i]=0; perebor(i+1, chosen, sum)Код на Python
def encode(limit_i):
"""
Строим минимальный шифр для текущих used[0..limit_i-1].
Для букв с индексом >= limit_i считаем, что они длинные (даже если где-то осталось used=1).
"""
code_for_letter = [""] * k
ns = 0 # какой SHORT выдаём следующий
nl = 0 # какой LONG выдаём следующий
out = []
for ch in s:
idx = idx_of[ch]
if code_for_letter[idx] == "":
is_short = (idx < limit_i and used[idx] == 1)
if is_short:
code_for_letter[idx] = SHORT[ns]
ns += 1
else:
code_for_letter[idx] = LONG[nl]
nl += 1
out.append(code_for_letter[idx])
return "".join(out)
def perebor(i, chosen_short, sum_short):
# 1) Если уже выбрали 9 коротких, то остальные автоматически длинные
if chosen_short == 9:
if sum_short == BEST_SUM:
cand = encode(i)
if best[0] is None or cand < best[0]:
best[0] = cand
return
# 2) Если дошли до конца — не смогли набрать 9
if i == k:
return
# 3) Отсечение: даже если взять все оставшиеся, 9 не наберём
if chosen_short + (k - i) < 9:
return
# 4) Отсечение по сумме частот: даже в лучшем случае не догоним BEST_SUM
need = 9 - chosen_short
# так как letters отсортированы по убыванию частоты, максимум добора = сумма cnt[i..i+need-1]
max_add = pref[i + need] - pref[i]
if sum_short + max_add < BEST_SUM:
return
# Вариант A: берём letters[i] как короткую
used[i] = 1
perebor(i + 1, chosen_short + 1, sum_short + cnt[i])
# Вариант B: не берём (значит длинная)
used[i] = 0
perebor(i + 1, chosen_short, sum_short)
SHORT = ["1", "2", "3", "4", "5", "6", "7", "8", "9"]
LONG = ["10", "20", "30", "40", "50", "60", "70", "80", "90"]
s = input()
# 1) Частоты и список разных букв
cnt = {}
for ch in s:
cnt[ch] = cnt.get(ch, 0) + 1
letters = list(cnt.keys())
k = len(letters)
# Если букв <= 9: все могут быть короткими -> просто жадно по первому появлению
if k <= 9:
code = {}
next_short = 0
out = []
for ch in s:
if ch not in code:
code[ch] = SHORT[next_short]
next_short += 1
out.append(code[ch])
print("".join(out))
else:
# 2) Сортируем буквы по убыванию частоты (удобно для отсечений)
letters.sort(key=lambda ch: -cnt[ch])
cnt = [cnt[ch] for ch in letters] # частоты в этом порядке
# BEST_SUM = сумма частот 9 самых частых букв -> минимальная длина
tmp = cnt[:]
tmp.sort(reverse=True)
BEST_SUM = sum(tmp[:9])
# prefix суммы частот: pref[i] = cnt[0]+...+cnt[i-1]
pref = [0] * (k + 1)
for i in range(k):
pref[i + 1] = pref[i] + cnt[i]
# быстрый доступ: буква -> её индекс в letters
idx_of = {}
for i in range(k):
idx_of[letters[i]] = i
# used[i] = 1 если letters[i] короткая, иначе 0 (длинная)
used = [0] * k
best = [None] # лучший результат-строка
perebor(0, 0, 0)
print(best[0])
по математике
и программированию