



В большинстве задач принято писать сухие разборы. Здесь же будут порой задаваться вопросы: риторические и не только. Они помогут вам понять то, как же решается задача и / или почему именно такое решение. Как размышлять и прийти к решению. Постараемся не писать сложных фраз, сделаем все красиво и понятно. Приятного прочтения.
Если хотели бы получить разбор последней задачи, пожалуйста, проявите активность под статьёй или постом!
Задача А. Качели
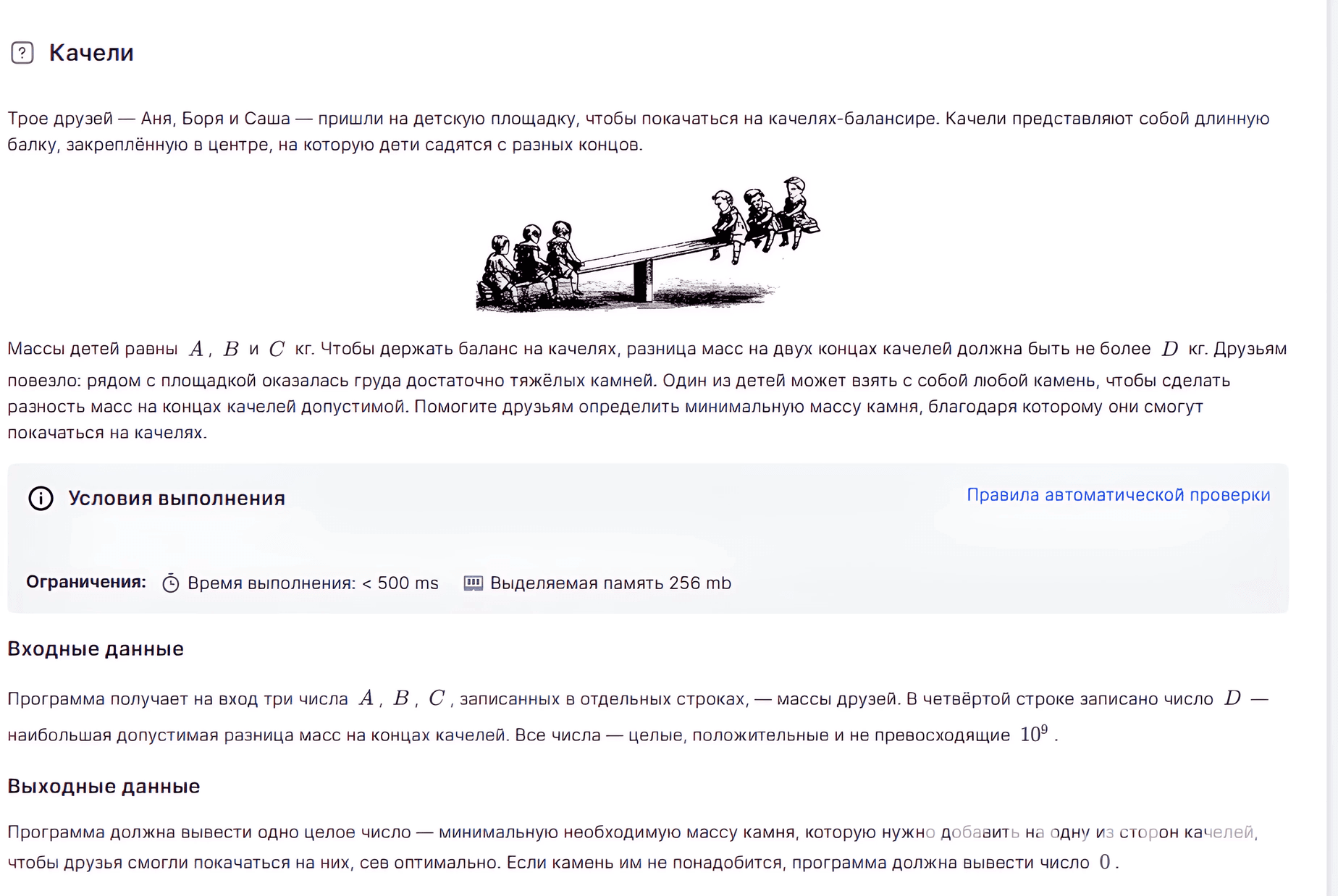

Наша с вами задача рассадить ребят так, чтобы разница между левыми и правыми качелями была минимальна.
Для начала поймем, что никогда невыгодно (да-да, нехорошее слово для математики, но в программирование это слово из темы жадность, часто будет всплывать) сажать трех ребят с одной стороны. Более того, тогда и камень нет смысла брать и, если их суммарный вес больше, чем D, то уменьшить его не получится.
Так как выгоднее посадить двух ребят с одной стороны и одного с третьей, чтобы разница была минимальной?
В таких случаях всегда проще предполагать, что A ≤ B ≤ C - то есть A — самый легкий из ребят, а С — самый тяжелый. При том, если вес у всех одинаковый, то А = В = С и, по сути, все равно можно сказать, что А — самый легкий, а С — самый тяжелый.
Соответственно, практически очевидно, что выгодно посадить A + B с одной стороны, а С с другой, тогда разница между ними будет минимальной. Далее нужно понять, кому взять камень, а кому нет. Возможно, С окажется настолько тяжелым, что будет сильно превосходить вес А и В суммарно, а возможно, все же недостаточно. И наоборот А + В в сумме будут весить, больше чем С на столько, что придется брать камень.
Итог: действуем просто — упорядочиваем так, чтобы A ≤ B ≤ C и далее смотрим кто больше: A + B или С
Если разница между этими двумя значениями больше D, то мы можем посчитать какой камень нам нужен. Код ниже.
Задача А. 100 баллов
a, b, c, d = int(input()), int(input()), int(input()), int(input())
kids = [a, b, c]
kids.sort()
if kids[0] + kids[1] >= kids[2]:
delta = kids[0] + kids[1] - kids[2]
else:
delta = kids[2] - kids[0] - kids[1]
print(max(0, delta - d))Задача В. Фонари.


Опишем сразу решение на 100.
Опять же посмотрим как ВЫГОДНЕЕ расставлять фонари? Конечно, мы будем сначала ставить те фонари, что светят больше. Но как мы их расставим?
Давайте рассмотрим пример и далее решим в общих числах (так постоянно делают программисты). Пусть есть серия фонарей, что светят на 3 вдаль. То есть на то, где поставили, на 3 влево и на 3 вправо. Куда выгодно поставить его в начале? Предполагаем, что N огромное = 1000.
Конечно, нам надо, чтобы были освещены 1 + 2 + 3 позиции, соответственно, поставим на позицию 4 (1 + 3). Заметим, что освещение теперь есть с 1 - 3 + 4 + 5 - 7. Следующий фонарь будет и должен освещать 8 - 10 + 11 + 12 - 14 позиции. То есть заметим, первый поставили на позицию 4 - следующий на 4 + 3 + 3 + 1 = 11 позицию. То есть если первый мы поставим на позицию A + 1 → следующий будет на позиции A + 1 + (2 * A + 1). Далее снова сдвинем на 2 * A + 1 и так далее, пока либо не кончатся все фонари, либо мы не заполним всю улицу фонарями. Далее уже будем использовать менее выгодные фонари.
Итогово алгоритм состоит из трех этапов:
Поменять местами фонари, чтобы первый (А) был выгоднее второго (В). Не забыть поменять количество фонарей соответствующего типа.
Начать расставлять фонари типа А, пока не кончатся, либо пока не заполним всю улицу. Далее расставляем все фонари В, если улица все еще не полностью в фонарном свете.
В конце надо проверить, смогли ли все расставить. Если нет, то вывести соответствующий ответ. Иначе вывести расстановку.
Задача В. Пример расстановки фонарей: сила свечения = 3

Задача В
n = int(input())
a, x, b, y = map(int, input().split())
# мы хотим, чтобы x >= y, то есть x более выгодный фонарик
if x < y:
x, y = y, x
a, b = b, a
ans = []
r = 1 # позиция где у нас пока не светит фонарь
while r <= n and a > 0:
next_f = min(r + x, n) # расставляем фонари, что светят на X
ans.append((next_f, x))
# добавляем позицию фонаря и тип фонаря
r += 2 * x + 1
# сдвигаемся к следующей позиции, что не освещена
a -= 1
# аналогично если все еще не освещена улица полностью - расставляем вторые фонари
while r <= n and b > 0:
next_f = min(r + y, n)
ans.append((next_f, y))
r += 2 * y + 1
b -= 1
# Если все еще есть что-то не освещенное - то выводим -1 - не смогли осветить все
if r <= n:
print(-1)
else:
print(len(ans))
for i in range(0, len(ans)):
# тут первое это позиция фонаря и тип фонаря
print(ans[i][0], ans[i][1])Задача С. Красная шапочка на болоте.


Для начала нужно понять, что никогда не бывает выгодно наступать на полянки, которые имеют отрицательные задачи. Но нам всегда выгодно наступить на положительную полянку. Итоговое решение становится почти очевидным: идем слева направо и передвигаемся только по положительным полянкам. Если в один момент до новой полянки мы не можем допрыгнуть = не хватает энергии, то и дальше никуда прыгнуть мы не можем. В конце либо нам хватит допрыгнуть до позиции N + 1, либо нет. Если да, то выводим сколько энергии останется, если нет, то соответствующий ответ.
Задача С
e = int(input())
n = int(input())
a = [0] * (n + 1)
for i in range(1, n + 1):
a[i] = int(input())
cur = 0 # на какой полянке мы сейчас находимся
for i in range(1, n + 1):
# если энергия положительна и мы можем допрыгнуть до этой позиции - то прыгаем
if a[i] > 0 and i - cur <= e:
e += a[i] - (i - cur) # добавляем энергию
cur = i # сохраняем позицию где теперь оказались
if n + 1 - cur <= e: # если мы можем допрыгнуть с последней полянки - то прыгаем
# n + 1 - cur - столько энергии мы потратим
print(e - (n + 1 - cur))
else:
print(-1)Задача D. Деление шоколадки.

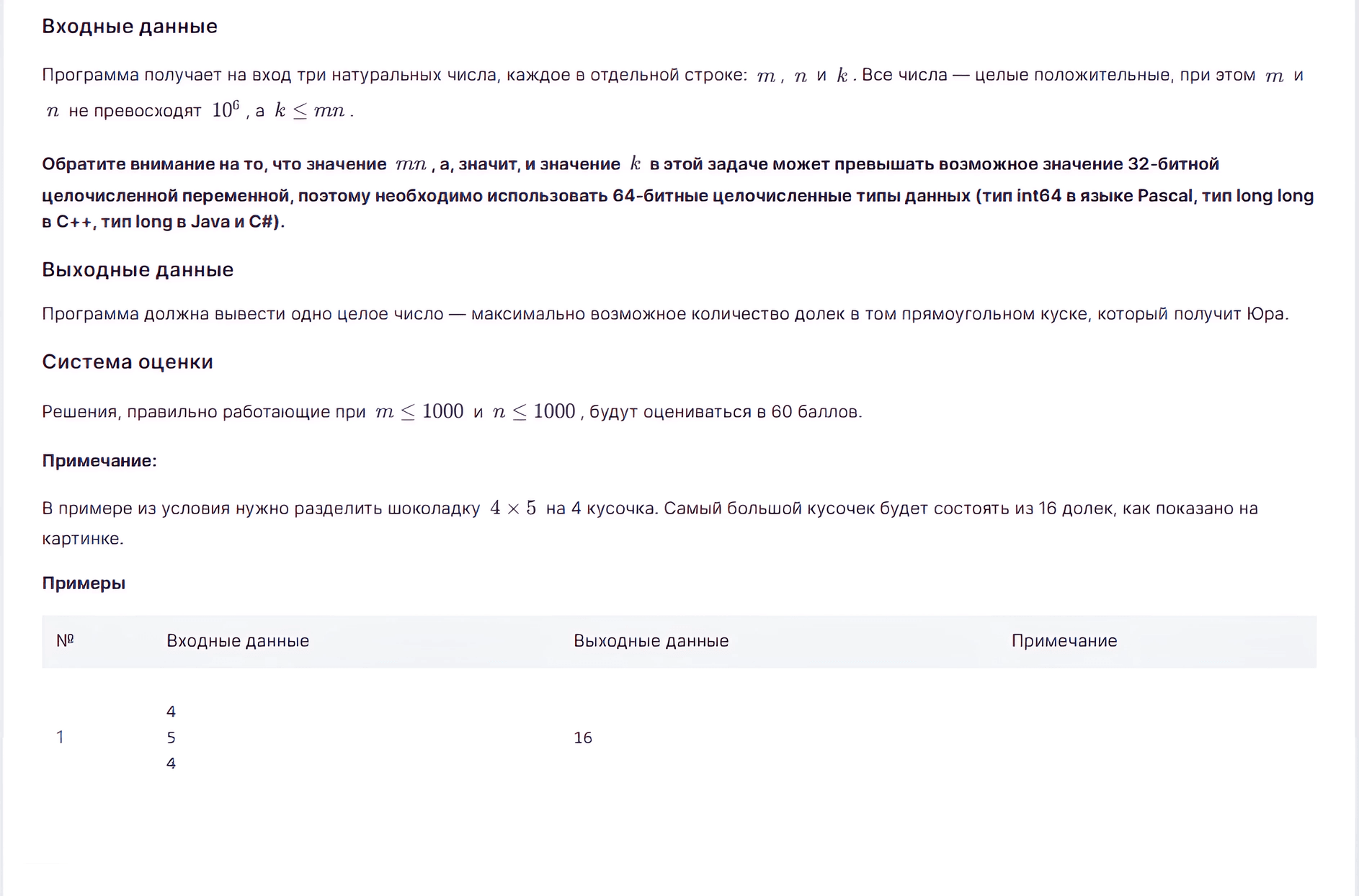
Самое сложное в этой задаче осознать два факта. Вот у нас в конце остается прямоугольник размера W по ширине, H - по высоте. Начальная ширина, напомним, M и высота — N.
То есть, по сути, оставшаяся площадь у нас M * N - H * W. При этом данные кусочки можно разделить на 1 на 1 и получить ровно столько кусочков плитки. Нам нужно, чтобы K ≤ M * N - H * W. Отсюда сразу легко понять решение на 60 - переберем потенциальную H - высоту, и затем переберем W - ширину. Те, что H и W нам подходят — из них надо выбрать такие параметры, чтобы площадь была максимальной. Это называется перебор. Работает он за N * M действий и проходит по ограничения на 60 баллов (на С++ точно).
Важно помнить, что питон может выполнить 2 - 4 миллиона операций за секунду (у нас секунда ограничение по времени), а С++ около 200 млн операций. На 100 баллов не зайдет, так как 100 тыс * 100 тыс = 10^10 = 10 миллиардов… Немного много
Задача D. Пример к разбору
Задача D. 60 баллов
m, n, k = int(input()), int(input()), int(input())
ans = 0
for i in range(1, n + 1): # перебираем высоту
for j in range(1, m + 1): # перебираем ширину
# отрезанная площадь должна быть хотя бы k и ширина умножить на высоту больше,
# чем то что мы сохранили ранее
if n * m - i * j >= k and i * j >= ans:
ans = i * j
print(ans)Как же улучшить его до 100 баллов?
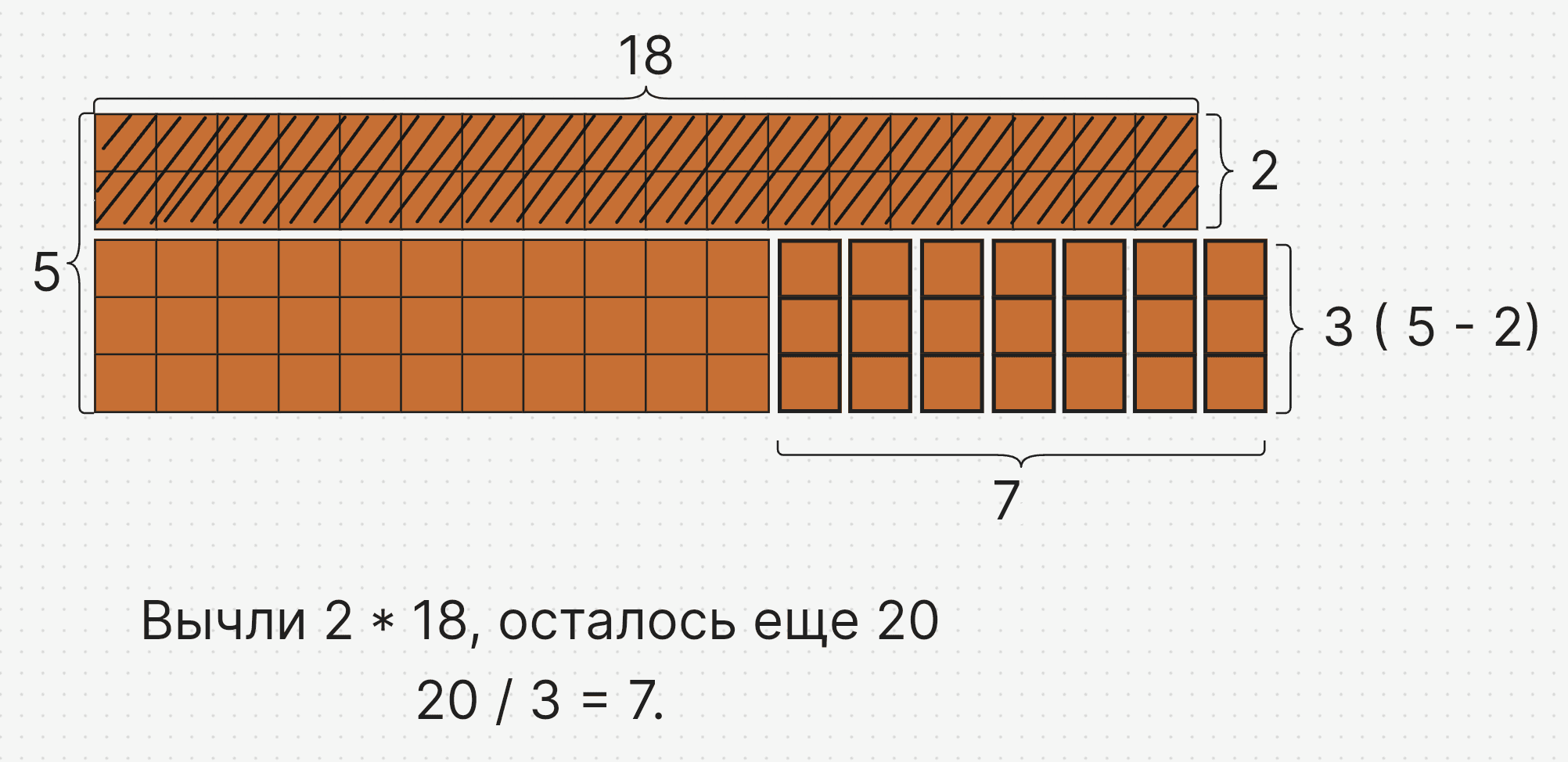
Давайте осознаем следующее, мы сначала перебираем высоту. То есть, по сути, мы отрезали сколько-то строчек. Каждая строка по M в ширину - то есть отрезано i * M блоков шоколада. То есть нам теоретически надо еще k - i * M шоколада (если это число больше нуля).
Далее мы отрезаем, получается, вертикальные слайсы каждый из которых по N - i в высоту. Соответсвенно, если нам надо еще 20, а мы из высоты 5 отрезали 2 строки - то в высоту мы отрезаем по 3. Получается 20 / 3 еще 7 вертикальных разрезов в ширину придется отрезать.
Получается, что так мы не должны перебирать ширину, мы можем фиксировать высоту и исходя из нее вычислять сколько минимально надо еще отрезать в ширину, чтобы нам хватило количество на нужное количество k.
Фраза не самая простая, всем программистам надо научиться читать подобный текст + смотрите на картинку и код — тогда станет в разы понятнее. Это p.s. то есть постскриптум, должен успокоить вас, если вдруг испугались.
Помните, вам может быть сложно осилить решение каждой задачи, и это решение уже на некий солидный уровень знаний / умений. Если не можете осилить здесь и сейчас легко, не переживайте, смело ее пропускаете и вернетесь к ней когда-нибудь в будущем.
Финально резюмируем: зная высоту мы вычисляем ширину, опять же проверяем, чтобы площадь была наибольшей из возможных. Смотрите ниже код на 100.
Задача D. 100 баллов
m, n, k = int(input()), int(input()), int(input())
ans = 0
for i in range(0, n):
more_m = (k - i * m) // (n - i)
if more_m % (n - i) != 0:
more_m += 1
cur_s = (n - i) * (m - more_m)
if cur_s > ans and more_m >= 0 and more_m <= m:
ans = cur_s
print(ans)В большинстве задач принято писать сухие разборы. Здесь же будут порой задаваться вопросы: риторические и не только. Они помогут вам понять то, как же решается задача и / или почему именно такое решение. Как размышлять и прийти к решению. Постараемся не писать сложных фраз, сделаем все красиво и понятно. Приятного прочтения.
Если хотели бы получить разбор последней задачи, пожалуйста, проявите активность под статьёй или постом!
Задача А. Качели


Наша с вами задача рассадить ребят так, чтобы разница между левыми и правыми качелями была минимальна.
Для начала поймем, что никогда невыгодно (да-да, нехорошее слово для математики, но в программирование это слово из темы жадность, часто будет всплывать) сажать трех ребят с одной стороны. Более того, тогда и камень нет смысла брать и, если их суммарный вес больше, чем D, то уменьшить его не получится.
Так как выгоднее посадить двух ребят с одной стороны и одного с третьей, чтобы разница была минимальной?
В таких случаях всегда проще предполагать, что A ≤ B ≤ C - то есть A — самый легкий из ребят, а С — самый тяжелый. При том, если вес у всех одинаковый, то А = В = С и, по сути, все равно можно сказать, что А — самый легкий, а С — самый тяжелый.
Соответственно, практически очевидно, что выгодно посадить A + B с одной стороны, а С с другой, тогда разница между ними будет минимальной. Далее нужно понять, кому взять камень, а кому нет. Возможно, С окажется настолько тяжелым, что будет сильно превосходить вес А и В суммарно, а возможно, все же недостаточно. И наоборот А + В в сумме будут весить, больше чем С на столько, что придется брать камень.
Итог: действуем просто — упорядочиваем так, чтобы A ≤ B ≤ C и далее смотрим кто больше: A + B или С
Если разница между этими двумя значениями больше D, то мы можем посчитать какой камень нам нужен. Код ниже.
Задача А. 100 баллов
a, b, c, d = int(input()), int(input()), int(input()), int(input())
kids = [a, b, c]
kids.sort()
if kids[0] + kids[1] >= kids[2]:
delta = kids[0] + kids[1] - kids[2]
else:
delta = kids[2] - kids[0] - kids[1]
print(max(0, delta - d))Задача В. Фонари.


Опишем сразу решение на 100.
Опять же посмотрим как ВЫГОДНЕЕ расставлять фонари? Конечно, мы будем сначала ставить те фонари, что светят больше. Но как мы их расставим?
Давайте рассмотрим пример и далее решим в общих числах (так постоянно делают программисты). Пусть есть серия фонарей, что светят на 3 вдаль. То есть на то, где поставили, на 3 влево и на 3 вправо. Куда выгодно поставить его в начале? Предполагаем, что N огромное = 1000.
Конечно, нам надо, чтобы были освещены 1 + 2 + 3 позиции, соответственно, поставим на позицию 4 (1 + 3). Заметим, что освещение теперь есть с 1 - 3 + 4 + 5 - 7. Следующий фонарь будет и должен освещать 8 - 10 + 11 + 12 - 14 позиции. То есть заметим, первый поставили на позицию 4 - следующий на 4 + 3 + 3 + 1 = 11 позицию. То есть если первый мы поставим на позицию A + 1 → следующий будет на позиции A + 1 + (2 * A + 1). Далее снова сдвинем на 2 * A + 1 и так далее, пока либо не кончатся все фонари, либо мы не заполним всю улицу фонарями. Далее уже будем использовать менее выгодные фонари.
Итогово алгоритм состоит из трех этапов:
Поменять местами фонари, чтобы первый (А) был выгоднее второго (В). Не забыть поменять количество фонарей соответствующего типа.
Начать расставлять фонари типа А, пока не кончатся, либо пока не заполним всю улицу. Далее расставляем все фонари В, если улица все еще не полностью в фонарном свете.
В конце надо проверить, смогли ли все расставить. Если нет, то вывести соответствующий ответ. Иначе вывести расстановку.
Задача В. Пример расстановки фонарей: сила свечения = 3

Задача В
n = int(input())
a, x, b, y = map(int, input().split())
# мы хотим, чтобы x >= y, то есть x более выгодный фонарик
if x < y:
x, y = y, x
a, b = b, a
ans = []
r = 1 # позиция где у нас пока не светит фонарь
while r <= n and a > 0:
next_f = min(r + x, n) # расставляем фонари, что светят на X
ans.append((next_f, x))
# добавляем позицию фонаря и тип фонаря
r += 2 * x + 1
# сдвигаемся к следующей позиции, что не освещена
a -= 1
# аналогично если все еще не освещена улица полностью - расставляем вторые фонари
while r <= n and b > 0:
next_f = min(r + y, n)
ans.append((next_f, y))
r += 2 * y + 1
b -= 1
# Если все еще есть что-то не освещенное - то выводим -1 - не смогли осветить все
if r <= n:
print(-1)
else:
print(len(ans))
for i in range(0, len(ans)):
# тут первое это позиция фонаря и тип фонаря
print(ans[i][0], ans[i][1])Задача С. Красная шапочка на болоте.


Для начала нужно понять, что никогда не бывает выгодно наступать на полянки, которые имеют отрицательные задачи. Но нам всегда выгодно наступить на положительную полянку. Итоговое решение становится почти очевидным: идем слева направо и передвигаемся только по положительным полянкам. Если в один момент до новой полянки мы не можем допрыгнуть = не хватает энергии, то и дальше никуда прыгнуть мы не можем. В конце либо нам хватит допрыгнуть до позиции N + 1, либо нет. Если да, то выводим сколько энергии останется, если нет, то соответствующий ответ.
Задача С
e = int(input())
n = int(input())
a = [0] * (n + 1)
for i in range(1, n + 1):
a[i] = int(input())
cur = 0 # на какой полянке мы сейчас находимся
for i in range(1, n + 1):
# если энергия положительна и мы можем допрыгнуть до этой позиции - то прыгаем
if a[i] > 0 and i - cur <= e:
e += a[i] - (i - cur) # добавляем энергию
cur = i # сохраняем позицию где теперь оказались
if n + 1 - cur <= e: # если мы можем допрыгнуть с последней полянки - то прыгаем
# n + 1 - cur - столько энергии мы потратим
print(e - (n + 1 - cur))
else:
print(-1)Задача D. Деление шоколадки.


Самое сложное в этой задаче осознать два факта. Вот у нас в конце остается прямоугольник размера W по ширине, H - по высоте. Начальная ширина, напомним, M и высота — N.
То есть, по сути, оставшаяся площадь у нас M * N - H * W. При этом данные кусочки можно разделить на 1 на 1 и получить ровно столько кусочков плитки. Нам нужно, чтобы K ≤ M * N - H * W. Отсюда сразу легко понять решение на 60 - переберем потенциальную H - высоту, и затем переберем W - ширину. Те, что H и W нам подходят — из них надо выбрать такие параметры, чтобы площадь была максимальной. Это называется перебор. Работает он за N * M действий и проходит по ограничения на 60 баллов (на С++ точно).
Важно помнить, что питон может выполнить 2 - 4 миллиона операций за секунду (у нас секунда ограничение по времени), а С++ около 200 млн операций. На 100 баллов не зайдет, так как 100 тыс * 100 тыс = 10^10 = 10 миллиардов… Немного много
Задача D. Пример к разбору

Задача D. 60 баллов
m, n, k = int(input()), int(input()), int(input())
ans = 0
for i in range(1, n + 1): # перебираем высоту
for j in range(1, m + 1): # перебираем ширину
# отрезанная площадь должна быть хотя бы k и ширина умножить на высоту больше,
# чем то что мы сохранили ранее
if n * m - i * j >= k and i * j >= ans:
ans = i * j
print(ans)Как же улучшить его до 100 баллов?
Давайте осознаем следующее, мы сначала перебираем высоту. То есть, по сути, мы отрезали сколько-то строчек. Каждая строка по M в ширину - то есть отрезано i * M блоков шоколада. То есть нам теоретически надо еще k - i * M шоколада (если это число больше нуля).
Далее мы отрезаем, получается, вертикальные слайсы каждый из которых по N - i в высоту. Соответсвенно, если нам надо еще 20, а мы из высоты 5 отрезали 2 строки - то в высоту мы отрезаем по 3. Получается 20 / 3 еще 7 вертикальных разрезов в ширину придется отрезать.
Получается, что так мы не должны перебирать ширину, мы можем фиксировать высоту и исходя из нее вычислять сколько минимально надо еще отрезать в ширину, чтобы нам хватило количество на нужное количество k.
Фраза не самая простая, всем программистам надо научиться читать подобный текст + смотрите на картинку и код — тогда станет в разы понятнее. Это p.s. то есть постскриптум, должен успокоить вас, если вдруг испугались.
Помните, вам может быть сложно осилить решение каждой задачи, и это решение уже на некий солидный уровень знаний / умений. Если не можете осилить здесь и сейчас легко, не переживайте, смело ее пропускаете и вернетесь к ней когда-нибудь в будущем.
Финально резюмируем: зная высоту мы вычисляем ширину, опять же проверяем, чтобы площадь была наибольшей из возможных. Смотрите ниже код на 100.
Задача D. 100 баллов
m, n, k = int(input()), int(input()), int(input())
ans = 0
for i in range(0, n):
more_m = (k - i * m) // (n - i)
if more_m % (n - i) != 0:
more_m += 1
cur_s = (n - i) * (m - more_m)
if cur_s > ans and more_m >= 0 and more_m <= m:
ans = cur_s
print(ans)В большинстве задач принято писать сухие разборы. Здесь же будут порой задаваться вопросы: риторические и не только. Они помогут вам понять то, как же решается задача и / или почему именно такое решение. Как размышлять и прийти к решению. Постараемся не писать сложных фраз, сделаем все красиво и понятно. Приятного прочтения.
Если хотели бы получить разбор последней задачи, пожалуйста, проявите активность под статьёй или постом!
Задача А. Качели


Наша с вами задача рассадить ребят так, чтобы разница между левыми и правыми качелями была минимальна.
Для начала поймем, что никогда невыгодно (да-да, нехорошее слово для математики, но в программирование это слово из темы жадность, часто будет всплывать) сажать трех ребят с одной стороны. Более того, тогда и камень нет смысла брать и, если их суммарный вес больше, чем D, то уменьшить его не получится.
Так как выгоднее посадить двух ребят с одной стороны и одного с третьей, чтобы разница была минимальной?
В таких случаях всегда проще предполагать, что A ≤ B ≤ C - то есть A — самый легкий из ребят, а С — самый тяжелый. При том, если вес у всех одинаковый, то А = В = С и, по сути, все равно можно сказать, что А — самый легкий, а С — самый тяжелый.
Соответственно, практически очевидно, что выгодно посадить A + B с одной стороны, а С с другой, тогда разница между ними будет минимальной. Далее нужно понять, кому взять камень, а кому нет. Возможно, С окажется настолько тяжелым, что будет сильно превосходить вес А и В суммарно, а возможно, все же недостаточно. И наоборот А + В в сумме будут весить, больше чем С на столько, что придется брать камень.
Итог: действуем просто — упорядочиваем так, чтобы A ≤ B ≤ C и далее смотрим кто больше: A + B или С
Если разница между этими двумя значениями больше D, то мы можем посчитать какой камень нам нужен. Код ниже.
Задача А. 100 баллов
a, b, c, d = int(input()), int(input()), int(input()), int(input())
kids = [a, b, c]
kids.sort()
if kids[0] + kids[1] >= kids[2]:
delta = kids[0] + kids[1] - kids[2]
else:
delta = kids[2] - kids[0] - kids[1]
print(max(0, delta - d))Задача В. Фонари.


Опишем сразу решение на 100.
Опять же посмотрим как ВЫГОДНЕЕ расставлять фонари? Конечно, мы будем сначала ставить те фонари, что светят больше. Но как мы их расставим?
Давайте рассмотрим пример и далее решим в общих числах (так постоянно делают программисты). Пусть есть серия фонарей, что светят на 3 вдаль. То есть на то, где поставили, на 3 влево и на 3 вправо. Куда выгодно поставить его в начале? Предполагаем, что N огромное = 1000.
Конечно, нам надо, чтобы были освещены 1 + 2 + 3 позиции, соответственно, поставим на позицию 4 (1 + 3). Заметим, что освещение теперь есть с 1 - 3 + 4 + 5 - 7. Следующий фонарь будет и должен освещать 8 - 10 + 11 + 12 - 14 позиции. То есть заметим, первый поставили на позицию 4 - следующий на 4 + 3 + 3 + 1 = 11 позицию. То есть если первый мы поставим на позицию A + 1 → следующий будет на позиции A + 1 + (2 * A + 1). Далее снова сдвинем на 2 * A + 1 и так далее, пока либо не кончатся все фонари, либо мы не заполним всю улицу фонарями. Далее уже будем использовать менее выгодные фонари.
Итогово алгоритм состоит из трех этапов:
Поменять местами фонари, чтобы первый (А) был выгоднее второго (В). Не забыть поменять количество фонарей соответствующего типа.
Начать расставлять фонари типа А, пока не кончатся, либо пока не заполним всю улицу. Далее расставляем все фонари В, если улица все еще не полностью в фонарном свете.
В конце надо проверить, смогли ли все расставить. Если нет, то вывести соответствующий ответ. Иначе вывести расстановку.
Задача В. Пример расстановки фонарей: сила свечения = 3

Задача В
n = int(input())
a, x, b, y = map(int, input().split())
# мы хотим, чтобы x >= y, то есть x более выгодный фонарик
if x < y:
x, y = y, x
a, b = b, a
ans = []
r = 1 # позиция где у нас пока не светит фонарь
while r <= n and a > 0:
next_f = min(r + x, n) # расставляем фонари, что светят на X
ans.append((next_f, x))
# добавляем позицию фонаря и тип фонаря
r += 2 * x + 1
# сдвигаемся к следующей позиции, что не освещена
a -= 1
# аналогично если все еще не освещена улица полностью - расставляем вторые фонари
while r <= n and b > 0:
next_f = min(r + y, n)
ans.append((next_f, y))
r += 2 * y + 1
b -= 1
# Если все еще есть что-то не освещенное - то выводим -1 - не смогли осветить все
if r <= n:
print(-1)
else:
print(len(ans))
for i in range(0, len(ans)):
# тут первое это позиция фонаря и тип фонаря
print(ans[i][0], ans[i][1])Задача С. Красная шапочка на болоте.


Для начала нужно понять, что никогда не бывает выгодно наступать на полянки, которые имеют отрицательные задачи. Но нам всегда выгодно наступить на положительную полянку. Итоговое решение становится почти очевидным: идем слева направо и передвигаемся только по положительным полянкам. Если в один момент до новой полянки мы не можем допрыгнуть = не хватает энергии, то и дальше никуда прыгнуть мы не можем. В конце либо нам хватит допрыгнуть до позиции N + 1, либо нет. Если да, то выводим сколько энергии останется, если нет, то соответствующий ответ.
Задача С
e = int(input())
n = int(input())
a = [0] * (n + 1)
for i in range(1, n + 1):
a[i] = int(input())
cur = 0 # на какой полянке мы сейчас находимся
for i in range(1, n + 1):
# если энергия положительна и мы можем допрыгнуть до этой позиции - то прыгаем
if a[i] > 0 and i - cur <= e:
e += a[i] - (i - cur) # добавляем энергию
cur = i # сохраняем позицию где теперь оказались
if n + 1 - cur <= e: # если мы можем допрыгнуть с последней полянки - то прыгаем
# n + 1 - cur - столько энергии мы потратим
print(e - (n + 1 - cur))
else:
print(-1)Задача D. Деление шоколадки.


Самое сложное в этой задаче осознать два факта. Вот у нас в конце остается прямоугольник размера W по ширине, H - по высоте. Начальная ширина, напомним, M и высота — N.
То есть, по сути, оставшаяся площадь у нас M * N - H * W. При этом данные кусочки можно разделить на 1 на 1 и получить ровно столько кусочков плитки. Нам нужно, чтобы K ≤ M * N - H * W. Отсюда сразу легко понять решение на 60 - переберем потенциальную H - высоту, и затем переберем W - ширину. Те, что H и W нам подходят — из них надо выбрать такие параметры, чтобы площадь была максимальной. Это называется перебор. Работает он за N * M действий и проходит по ограничения на 60 баллов (на С++ точно).
Важно помнить, что питон может выполнить 2 - 4 миллиона операций за секунду (у нас секунда ограничение по времени), а С++ около 200 млн операций. На 100 баллов не зайдет, так как 100 тыс * 100 тыс = 10^10 = 10 миллиардов… Немного много
Задача D. Пример к разбору

Задача D. 60 баллов
m, n, k = int(input()), int(input()), int(input())
ans = 0
for i in range(1, n + 1): # перебираем высоту
for j in range(1, m + 1): # перебираем ширину
# отрезанная площадь должна быть хотя бы k и ширина умножить на высоту больше,
# чем то что мы сохранили ранее
if n * m - i * j >= k and i * j >= ans:
ans = i * j
print(ans)Как же улучшить его до 100 баллов?
Давайте осознаем следующее, мы сначала перебираем высоту. То есть, по сути, мы отрезали сколько-то строчек. Каждая строка по M в ширину - то есть отрезано i * M блоков шоколада. То есть нам теоретически надо еще k - i * M шоколада (если это число больше нуля).
Далее мы отрезаем, получается, вертикальные слайсы каждый из которых по N - i в высоту. Соответсвенно, если нам надо еще 20, а мы из высоты 5 отрезали 2 строки - то в высоту мы отрезаем по 3. Получается 20 / 3 еще 7 вертикальных разрезов в ширину придется отрезать.
Получается, что так мы не должны перебирать ширину, мы можем фиксировать высоту и исходя из нее вычислять сколько минимально надо еще отрезать в ширину, чтобы нам хватило количество на нужное количество k.
Фраза не самая простая, всем программистам надо научиться читать подобный текст + смотрите на картинку и код — тогда станет в разы понятнее. Это p.s. то есть постскриптум, должен успокоить вас, если вдруг испугались.
Помните, вам может быть сложно осилить решение каждой задачи, и это решение уже на некий солидный уровень знаний / умений. Если не можете осилить здесь и сейчас легко, не переживайте, смело ее пропускаете и вернетесь к ней когда-нибудь в будущем.
Финально резюмируем: зная высоту мы вычисляем ширину, опять же проверяем, чтобы площадь была наибольшей из возможных. Смотрите ниже код на 100.
Задача D. 100 баллов
m, n, k = int(input()), int(input()), int(input())
ans = 0
for i in range(0, n):
more_m = (k - i * m) // (n - i)
if more_m % (n - i) != 0:
more_m += 1
cur_s = (n - i) * (m - more_m)
if cur_s > ans and more_m >= 0 and more_m <= m:
ans = cur_s
print(ans)В большинстве задач принято писать сухие разборы. Здесь же будут порой задаваться вопросы: риторические и не только. Они помогут вам понять то, как же решается задача и / или почему именно такое решение. Как размышлять и прийти к решению. Постараемся не писать сложных фраз, сделаем все красиво и понятно. Приятного прочтения.
Если хотели бы получить разбор последней задачи, пожалуйста, проявите активность под статьёй или постом!
Задача А. Качели


Наша с вами задача рассадить ребят так, чтобы разница между левыми и правыми качелями была минимальна.
Для начала поймем, что никогда невыгодно (да-да, нехорошее слово для математики, но в программирование это слово из темы жадность, часто будет всплывать) сажать трех ребят с одной стороны. Более того, тогда и камень нет смысла брать и, если их суммарный вес больше, чем D, то уменьшить его не получится.
Так как выгоднее посадить двух ребят с одной стороны и одного с третьей, чтобы разница была минимальной?
В таких случаях всегда проще предполагать, что A ≤ B ≤ C - то есть A — самый легкий из ребят, а С — самый тяжелый. При том, если вес у всех одинаковый, то А = В = С и, по сути, все равно можно сказать, что А — самый легкий, а С — самый тяжелый.
Соответственно, практически очевидно, что выгодно посадить A + B с одной стороны, а С с другой, тогда разница между ними будет минимальной. Далее нужно понять, кому взять камень, а кому нет. Возможно, С окажется настолько тяжелым, что будет сильно превосходить вес А и В суммарно, а возможно, все же недостаточно. И наоборот А + В в сумме будут весить, больше чем С на столько, что придется брать камень.
Итог: действуем просто — упорядочиваем так, чтобы A ≤ B ≤ C и далее смотрим кто больше: A + B или С
Если разница между этими двумя значениями больше D, то мы можем посчитать какой камень нам нужен. Код ниже.
Задача А. 100 баллов
a, b, c, d = int(input()), int(input()), int(input()), int(input())
kids = [a, b, c]
kids.sort()
if kids[0] + kids[1] >= kids[2]:
delta = kids[0] + kids[1] - kids[2]
else:
delta = kids[2] - kids[0] - kids[1]
print(max(0, delta - d))Задача В. Фонари.


Опишем сразу решение на 100.
Опять же посмотрим как ВЫГОДНЕЕ расставлять фонари? Конечно, мы будем сначала ставить те фонари, что светят больше. Но как мы их расставим?
Давайте рассмотрим пример и далее решим в общих числах (так постоянно делают программисты). Пусть есть серия фонарей, что светят на 3 вдаль. То есть на то, где поставили, на 3 влево и на 3 вправо. Куда выгодно поставить его в начале? Предполагаем, что N огромное = 1000.
Конечно, нам надо, чтобы были освещены 1 + 2 + 3 позиции, соответственно, поставим на позицию 4 (1 + 3). Заметим, что освещение теперь есть с 1 - 3 + 4 + 5 - 7. Следующий фонарь будет и должен освещать 8 - 10 + 11 + 12 - 14 позиции. То есть заметим, первый поставили на позицию 4 - следующий на 4 + 3 + 3 + 1 = 11 позицию. То есть если первый мы поставим на позицию A + 1 → следующий будет на позиции A + 1 + (2 * A + 1). Далее снова сдвинем на 2 * A + 1 и так далее, пока либо не кончатся все фонари, либо мы не заполним всю улицу фонарями. Далее уже будем использовать менее выгодные фонари.
Итогово алгоритм состоит из трех этапов:
Поменять местами фонари, чтобы первый (А) был выгоднее второго (В). Не забыть поменять количество фонарей соответствующего типа.
Начать расставлять фонари типа А, пока не кончатся, либо пока не заполним всю улицу. Далее расставляем все фонари В, если улица все еще не полностью в фонарном свете.
В конце надо проверить, смогли ли все расставить. Если нет, то вывести соответствующий ответ. Иначе вывести расстановку.
Задача В. Пример расстановки фонарей: сила свечения = 3

Задача В
n = int(input())
a, x, b, y = map(int, input().split())
# мы хотим, чтобы x >= y, то есть x более выгодный фонарик
if x < y:
x, y = y, x
a, b = b, a
ans = []
r = 1 # позиция где у нас пока не светит фонарь
while r <= n and a > 0:
next_f = min(r + x, n) # расставляем фонари, что светят на X
ans.append((next_f, x))
# добавляем позицию фонаря и тип фонаря
r += 2 * x + 1
# сдвигаемся к следующей позиции, что не освещена
a -= 1
# аналогично если все еще не освещена улица полностью - расставляем вторые фонари
while r <= n and b > 0:
next_f = min(r + y, n)
ans.append((next_f, y))
r += 2 * y + 1
b -= 1
# Если все еще есть что-то не освещенное - то выводим -1 - не смогли осветить все
if r <= n:
print(-1)
else:
print(len(ans))
for i in range(0, len(ans)):
# тут первое это позиция фонаря и тип фонаря
print(ans[i][0], ans[i][1])Задача С. Красная шапочка на болоте.


Для начала нужно понять, что никогда не бывает выгодно наступать на полянки, которые имеют отрицательные задачи. Но нам всегда выгодно наступить на положительную полянку. Итоговое решение становится почти очевидным: идем слева направо и передвигаемся только по положительным полянкам. Если в один момент до новой полянки мы не можем допрыгнуть = не хватает энергии, то и дальше никуда прыгнуть мы не можем. В конце либо нам хватит допрыгнуть до позиции N + 1, либо нет. Если да, то выводим сколько энергии останется, если нет, то соответствующий ответ.
Задача С
e = int(input())
n = int(input())
a = [0] * (n + 1)
for i in range(1, n + 1):
a[i] = int(input())
cur = 0 # на какой полянке мы сейчас находимся
for i in range(1, n + 1):
# если энергия положительна и мы можем допрыгнуть до этой позиции - то прыгаем
if a[i] > 0 and i - cur <= e:
e += a[i] - (i - cur) # добавляем энергию
cur = i # сохраняем позицию где теперь оказались
if n + 1 - cur <= e: # если мы можем допрыгнуть с последней полянки - то прыгаем
# n + 1 - cur - столько энергии мы потратим
print(e - (n + 1 - cur))
else:
print(-1)Задача D. Деление шоколадки.


Самое сложное в этой задаче осознать два факта. Вот у нас в конце остается прямоугольник размера W по ширине, H - по высоте. Начальная ширина, напомним, M и высота — N.
То есть, по сути, оставшаяся площадь у нас M * N - H * W. При этом данные кусочки можно разделить на 1 на 1 и получить ровно столько кусочков плитки. Нам нужно, чтобы K ≤ M * N - H * W. Отсюда сразу легко понять решение на 60 - переберем потенциальную H - высоту, и затем переберем W - ширину. Те, что H и W нам подходят — из них надо выбрать такие параметры, чтобы площадь была максимальной. Это называется перебор. Работает он за N * M действий и проходит по ограничения на 60 баллов (на С++ точно).
Важно помнить, что питон может выполнить 2 - 4 миллиона операций за секунду (у нас секунда ограничение по времени), а С++ около 200 млн операций. На 100 баллов не зайдет, так как 100 тыс * 100 тыс = 10^10 = 10 миллиардов… Немного много
Задача D. Пример к разбору

Задача D. 60 баллов
m, n, k = int(input()), int(input()), int(input())
ans = 0
for i in range(1, n + 1): # перебираем высоту
for j in range(1, m + 1): # перебираем ширину
# отрезанная площадь должна быть хотя бы k и ширина умножить на высоту больше,
# чем то что мы сохранили ранее
if n * m - i * j >= k and i * j >= ans:
ans = i * j
print(ans)Как же улучшить его до 100 баллов?
Давайте осознаем следующее, мы сначала перебираем высоту. То есть, по сути, мы отрезали сколько-то строчек. Каждая строка по M в ширину - то есть отрезано i * M блоков шоколада. То есть нам теоретически надо еще k - i * M шоколада (если это число больше нуля).
Далее мы отрезаем, получается, вертикальные слайсы каждый из которых по N - i в высоту. Соответсвенно, если нам надо еще 20, а мы из высоты 5 отрезали 2 строки - то в высоту мы отрезаем по 3. Получается 20 / 3 еще 7 вертикальных разрезов в ширину придется отрезать.
Получается, что так мы не должны перебирать ширину, мы можем фиксировать высоту и исходя из нее вычислять сколько минимально надо еще отрезать в ширину, чтобы нам хватило количество на нужное количество k.
Фраза не самая простая, всем программистам надо научиться читать подобный текст + смотрите на картинку и код — тогда станет в разы понятнее. Это p.s. то есть постскриптум, должен успокоить вас, если вдруг испугались.
Помните, вам может быть сложно осилить решение каждой задачи, и это решение уже на некий солидный уровень знаний / умений. Если не можете осилить здесь и сейчас легко, не переживайте, смело ее пропускаете и вернетесь к ней когда-нибудь в будущем.
Финально резюмируем: зная высоту мы вычисляем ширину, опять же проверяем, чтобы площадь была наибольшей из возможных. Смотрите ниже код на 100.
Задача D. 100 баллов
m, n, k = int(input()), int(input()), int(input())
ans = 0
for i in range(0, n):
more_m = (k - i * m) // (n - i)
if more_m % (n - i) != 0:
more_m += 1
cur_s = (n - i) * (m - more_m)
if cur_s > ans and more_m >= 0 and more_m <= m:
ans = cur_s
print(ans)Понравилась статья?
Подпишись на Телеграм школы, чтобы не пропустить новые статьи и новости
